练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．化简：（x+y）2-3（x2-2y2）=-2x2+2xy+7y2．如果2x÷16y=8，则2x-8y=6．

    分析 先套用完全平方公式及去括号，再合并同类项即可化简原式；根据幂的运算由2x÷16y=8可得2x-4y=23，即x-4y=3，再整体代入可得．

    解答 解：（x+y）2-3（x2-2y2）=x2+2xy+y2-3x2+6y2
    =-2x2+2xy+7y2；
    ∵2x÷16y=8，即2x÷（24）y=8，2x÷24y=8，
    ∴2x-4y=23，
    ∴x-4y=3，
    则2x-8y=2（x-4y）=6，
    故答案为：-2x2+2xy+7y2，6．

    点评 本题主要考查整式的混合运算，熟练掌握整式的混合运算法则及根据幂的运算法则由2x÷16y=8得到2x-4y=23是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．直角三角形的两条直角边为a，b，则斜边上的高为（　　）
    A．$\frac{a+b}{2}$B．$\frac{{a}^{2}+{b}^{2}}{2}$
    C．$\frac{\sqrt{{a}^{2}-{b}^{2}}}{2}$D．$\frac{ab\sqrt{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．某人在高为30米的铁塔AB的塔顶A处，向正东方向观察地面上的C处和D处，俯角分别是30°和60°．如果B、D、C成一直线，那么C处和D处之间的距离，可以是下列数据中的（　　）
    A．20$\sqrt{3}$米B．30$\sqrt{3}$米C．40$\sqrt{3}$米D．50$\sqrt{3}$米

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，在△ABC中，AB=AC，AD=AE，∠BAD=30°，∠DEC是（　　）
    A．10°B．12.5°C．15°D．20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．若点A（1，y1），B（2，y2），C（3，y3）在反比例函数y=$\frac{{k}^{2}+1}{x}$的图象上，则（　　）
    A．y1＜y2＜y3B．y1＞y2＞y3C．y1＜y3＜y2D．y1=y2=y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

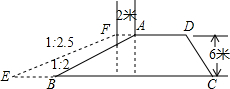    6．如图，有一段水库拦水坝，坝高6m，坝长50m，AD∥BC，沿水库拦水坝的背水坡将坝顶加宽2m，坡度由原来的1：2变成1：2.5．
    （1）求加宽部分横截面的面积．
    （2）完成这一工程需要多少立方米的土？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，-a，b，-b，a+b，a-b按照从小到大的顺序排列，正确的是（　　）
    A．a-b＜a＜-b＜b-a＜-a＜bB．-b＜a-b＜-a＜a＜b-a＜b
    C．a＜-b＜a-b＜-a＜b＜b-aD．a-b＜-b＜a＜-a＜b＜b-a

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．已知△ABC的周长为1，连接△ABC三边的中点构成第二个三角形，再连接第二个三角形三边的中点构成第三个三角形，依此类推，则第2014个三角形的周长为（　　）
    A．$\frac{1}{{2}^{2014}}$B．$\frac{1}{{2}^{2013}}$C．$\frac{1}{2014}$D．$\frac{1}{2013}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．等腰直角三角形ABC中，AB=AC，∠BAC=90°，D为BC中点，点F为AC边上一动点
    （1）如图1，若E为BF中点，连接DE，BF=13，AB=12，求DE的长度；
    （2）如图2，若F为AC中点，过A点作AG⊥BF垂足为点E，交BC于点G，取CG中点M，连接FM，FG，请判断BF，FM，FG之间的数量关系并证明；
    （3）当点F在AC上运动时，保持AG⊥BF垂足为点E，连接DE，∠DEG的度数会发生改变吗？如果不变请直接写出∠DEG的度数，如果改变请说明理由．

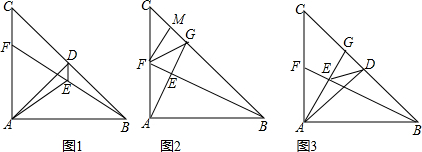
    查看答案和解析>>

    同步练习册答案