
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | y1≤y2 |
科目:初中数学 来源: 题型:解答题
 为了创建国家卫生城市,需要购买甲、乙(如图)两种类型的分类垃圾桶替换原来的垃圾桶,A,B,C三个小区所购买的数量和总价如表所示.
为了创建国家卫生城市,需要购买甲、乙(如图)两种类型的分类垃圾桶替换原来的垃圾桶,A,B,C三个小区所购买的数量和总价如表所示.| 甲型垃圾桶 数量(套) | 乙型垃圾桶 数量(套) | 总价(元) | |
| A | 10 | 8 | 3320 |
| B | 5 | 9 | 2860 |
| C | a | b | 2580 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=120°,则∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=120°,则∠2的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 生活经验:因为你在北半球,用走时准确的手表可以帮你辨别方向.将时针指向太阳所在方向,画它与12点夹角的平分线,这条平分线所指的方向就是南方,如图.
生活经验:因为你在北半球,用走时准确的手表可以帮你辨别方向.将时针指向太阳所在方向,画它与12点夹角的平分线,这条平分线所指的方向就是南方,如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
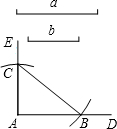 阅读下面材料:
阅读下面材料:| A. | HL | B. | SAS | C. | AAS | D. | SSA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com