
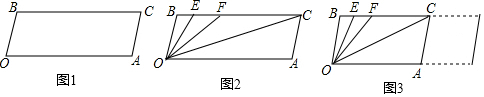
分析 (1)由BC∥OA得∠B+∠O=180°,所以∠O=180°-∠B=60°,则∠A+∠O=180°,根据平行线的判定即可得到OB∥AC;
(2)由OE平分∠BOF得到∠BOE=∠FOE,加上∠FOC=∠AOC,所以∠EOF+∠COF=$\frac{1}{2}$∠AOB=30°;
(3)由BC∥OA得到OCB=∠AOC,∠OFB=∠AOF,加上∠FOC=∠AOC,则∠AOF=2∠AOC,所以∠OFB=2∠OCB;
(4)设∠AOC的度数为x,则∠OFB=2x,根据平行线的性质得∠OEB=∠AOE,则∠OEB=∠EOC+∠AOC=30°+x,再根据三角形内角和定理得∠OCA=180°-∠AOC-∠A=60°-x,利用∠OEB=∠OCA得到30°+x=60°-x,解得x=15°,所以∠OCA=60°-x=45°.
解答 解:(1)∵BC∥OA,
∴∠B+∠O=180°,
∴∠O=180°-∠B=60°,
而∠A=120°,
∴∠A+∠O=180°,
∴OB∥AC;
(2)∵OE平分∠BOF,
∴∠BOE=∠FOE,
而∠FOC=∠AOC,
∴∠EOF+∠COF=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°,
即∠EOC=30°;
(3)比值不改变.
∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOF=2∠AOC,
∴∠OFB=2∠OCB,
即∠OCB:∠OFB的值为1:2;
(4)设∠AOC的度数为x,则∠OFB=2x,
∵∠OEB=∠AOE,
∴∠OEB=∠EOC+∠AOC=30°+x,
而∠OCA=180°-∠AOC-∠A=180°-x-120°=60°-x,
∵∠OEB=∠OCA,
∴30°+x=60°-x,
解得x=15°,
∴∠OCA=60°-x=60°-15°=45°.
点评 本题考查了平行线的判定与性质:同位角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.熟练掌握平行线的判定与性质是解本题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
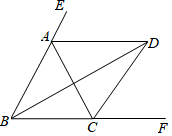 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC 外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ABC=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠ADC=$\frac{1}{2}$∠BAC.其中正确的结论有( )
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC 外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ABC=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;⑤∠ADC=$\frac{1}{2}$∠BAC.其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将一根绳子对折以后用线段AB表示,点P是AB的四等分点,现从P处将绳子剪断,剪断后的各段绳子中的一段长为30cm,则这条绳子的原长为40或80或120或240cm.
如图,将一根绳子对折以后用线段AB表示,点P是AB的四等分点,现从P处将绳子剪断,剪断后的各段绳子中的一段长为30cm,则这条绳子的原长为40或80或120或240cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com