练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
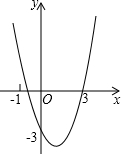
    12．如图，抛物线过（-1，0），（3，0），（0，-3）三点，沿x轴方向平移抛物线，使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，则符合条件的平移方式有（　　）
    A．1B．2C．3D．4

    分析 由抛物线与x轴的两交点之间的距离恒为4，结合平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，即可得出平移后的抛物线过点（0，-2），依此画出图形，利用数形结合即可得出结论．

    解答 解：∵抛物线与x轴的两交点之间的距离恒为3-（-1）=4，
    ∴当抛物线与y轴的交点为（0，-2）时，平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，
    ∴有两种平移方式，可使平移后的抛物线过点（0，-2）．
    故选B．

    点评 本题考查了抛物线与x轴的交点以及二次函数图象与几何变换，根据三角形的面积为4，找出平移后的抛物线过点（0，-2）是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年吉林省七年级下学期第一次月考数学试卷（解析版） 题型：解答题

    某同学在A、B两家超市发现他看中的学习机和书包的单价都相同，学习机和书包的单价之和为452元，且学习机的单价比书包单价的4倍少8元。 

    （1）学习机和书包的单价各是多少元？ 

    （2）该同学上街，恰好赶上该商品促销，超市A所有商品打八折销售，超市B全场购满100元返购物券30元销售，满200元返购物券60元，依次类推，（不足100元不返券，购物券全场通用），但他只带了390元钱，如果他只在一家超市购买他看中的这两样物品，你能说明他可以选择哪家购买更省钱吗?

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．在平面直角坐标系中．对于平面内任一点（m，n），规定以下两种变换：
    ①f（m，n）=（m，-n），如f（2，1）=（2，-1）；
    ②g（m，n）=（-m，-n），如g（2，1）=（-2，-1）．
    按照以上变换有：f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（3，2）]等于（　　）
    A．（3，2）B．（3．-2）C．（-3，2）D．（-3，-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：
    （1）（-x）•x2•（-x）6      
    （2）（y4）2÷（y2）3•y2
    （3）（-2a）3-（-a）•（3a）2           
    （4）（x-y）3•（x-y）2•（y-x）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．计算：$\frac{{1000}^{2}}{{625}^{2}{-375}^{2}}$=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．计算：|-2+1|=（　　）
    A．-1B．1C．-3D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知n是一个正整数，$\sqrt{12n}$是整数，则n的最小值是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

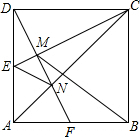    19．如图，在正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于点N，交AB于点F，连接EN、BM．有如下结论：①△ADF≌△DCE；②MN=FN；③△DMC∽△EMN；④BM=AB；其中正确结论的个数为（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．买书包和文具盒共50个，其中文具盒的数量是书包的3倍多2个，求书包和文具盒各买多少个？若设买书包x个，买文具盒y个，则列出的方程组应是（　　）
    A．$\left\{\begin{array}{l}{x+y=50}\\{x=3y-2}\end{array}\right.$B．$\left\{\begin{array}{l}{x+y=50}\\{x=3y+2}\end{array}\right.$C．$\left\{\begin{array}{l}{x+y=50}\\{y=3x-2}\end{array}\right.$D．$\left\{\begin{array}{l}{x+y=50}\\{y=3x+2}\end{array}\right.$

    查看答案和解析>>

    同步练习册答案