
分析 根据题意画出图形,分情况讨论即可.
解答 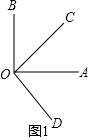 解:∠AOD与∠BOC相等或互补.理由如下:
解:∠AOD与∠BOC相等或互补.理由如下:
如图1,∵∠AOB=90°,∠COD=90°,
∴∠AOB=∠COD=90°,
∴∠COA+∠BOC=∠COA+∠AOD=90°,
∴∠BOC=∠AOD.
即∠AOD与∠BOC相等;
如图2,∵∠AOB=∠COD=90°,
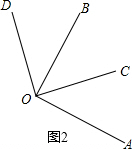 ∴∠AOC+∠BOC=90°,∠DOB+∠BOC=90°,
∴∠AOC+∠BOC=90°,∠DOB+∠BOC=90°,
∴∠AOC+∠BOC+∠DOB+∠BOC=90°+90°=180°,
∴∠AOD+∠BOC=180°,
即∠AOD与∠BOC互补;
如图3,∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=360°-∠AOB-∠COD=360°-90°-90°=180°,
即∠AOD与∠BOC互补.
点评 本题考查了余角和补角的定义,弄清各个角之间的关系是解题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
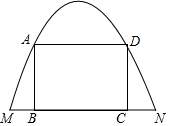 有一如图所示的纸片,拱形边缘呈抛物线形形状,MN=8米,抛物线顶点到边MN的距离是8米.点A和点D是抛物线上的两动点,且AD∥BC,过点A作AB⊥BC作DC⊥BC,过点B作DC⊥BC,点B、C在边MN上.
有一如图所示的纸片,拱形边缘呈抛物线形形状,MN=8米,抛物线顶点到边MN的距离是8米.点A和点D是抛物线上的两动点,且AD∥BC,过点A作AB⊥BC作DC⊥BC,过点B作DC⊥BC,点B、C在边MN上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,过点A做直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,则AE的长为11.9.
如图,在△ABC中,∠ACB=90°,过点A做直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,则AE的长为11.9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
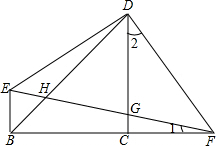 如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,
如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com