
【题目】如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
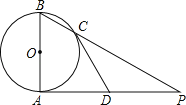
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
【答案】(1)AP=2![]() ;(2)见解析
;(2)见解析
【解析】
试题分析:(1)首先根据切线的性质判定∠BAP=90°;然后在直角三角形ABP中利用三角函数的定义求得AP的长度;
(2)连接OC,OD、AC构建全等三角形△OAD≌△OCD,然后利用全等三角形的对应角相等推知∠OAD=∠OCD=90°,即OC⊥CD.
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵AB=2,∠P=30°,
∴AP=![]() =
=![]() =2
=2![]() ,即AP=2
,即AP=2![]() ;
;
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
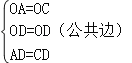 ,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】 如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
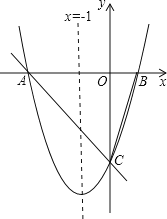
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将某样本数据分析整理后分成8组,且组距为5,画频数分布直方图时,求得某组的组中值恰好为18.则该组是( )
A. 10.5~15.5 B. 15.5~20.5
C. 20.5~25.5 D. 25.5~30.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com