
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+2的图象与x轴交于点A与反比例函数![]() (x<0)的图象交于点B,过点B作BC⊥x轴于点C,且OA=OC.
(x<0)的图象交于点B,过点B作BC⊥x轴于点C,且OA=OC.

(1)求点A的坐标和反比例函数的表达式;
(2)若点P是反比例函数![]() (x<0)的图象上的点,过P作PQ∥y轴,交直线AB于点Q,当PQ=BC时,求点P的坐标.
(x<0)的图象上的点,过P作PQ∥y轴,交直线AB于点Q,当PQ=BC时,求点P的坐标.
【答案】(1)A(2,0);![]() ;(2)(3﹣
;(2)(3﹣![]() ,3+
,3+![]() )或(﹣4,2).
)或(﹣4,2).
【解析】
(1)根据一次函数的解析式求得A的坐标,进而B点的横坐标,代入一次函数解析式求得纵坐标,得到B点的坐标,代入![]() 根据待定系数法即可求得反比例函数的解析式;
根据待定系数法即可求得反比例函数的解析式;
(2)设p(a,![]() )(a<0),则Q(a,-a+2),得到PQ=|
)(a<0),则Q(a,-a+2),得到PQ=|![]() -(-a+2)|=|
-(-a+2)|=|![]() +a-2=BC=4|,分两种情况讨论,列出关于a的方程,解方程即可求得.
+a-2=BC=4|,分两种情况讨论,列出关于a的方程,解方程即可求得.
解:(1)在y=﹣x+2中,当y=0时,﹣x+2=0,解得x=2,
∴A(2,0),
又OA=OC,
∴OC=OA=2,
又∵BC⊥x轴于点C,
∴B点的横坐标为﹣2,代入y=﹣x+2,可得B点的纵坐标为4,
∴点B坐标为(﹣2,4),
将点B坐标为(﹣2,4)代入![]() 得,
得,![]() ,
,
∴k=﹣8,
故反比例函数的表达式为![]() ;
;
(2)设P(a,![]() )(a<0),
)(a<0),
∵PQ∥y轴,交直线AB于点Q,
∴Q(a,﹣a+2),
∴PQ=|![]() ﹣(﹣a+2)|=|
﹣(﹣a+2)|=|![]() +a﹣2|,
+a﹣2|,
∵点B坐标为(﹣2,4),
∴BC=4,
当PQ=BC时,有![]() ,当﹣2<a<0时,有
,当﹣2<a<0时,有![]() ,
,
解之得![]() ,舍去正值,
,舍去正值,![]() ,此时点P(3﹣
,此时点P(3﹣![]() ,3+
,3+![]() ),
),
当a<﹣2时,有﹣![]() +a﹣2=﹣4,解之得a1=﹣4,a2=2(舍去),此时点P(﹣4,2),
+a﹣2=﹣4,解之得a1=﹣4,a2=2(舍去),此时点P(﹣4,2),
综上满足条件的点P坐标为(3﹣![]() ,3+
,3+![]() )或(﹣4,2).
)或(﹣4,2).


科目:初中数学 来源: 题型:
【题目】据天气预报报道,福建省部分城市某日的最高气温如下表所示:
城市 | 福州 | 厦门 | 宁德 | 莆田 | 泉州 | 漳州 | 龙岩 | 三明 | 南平 |
最高气温(℃) | 11 | 16 | 11 | 13 | 13 | 17 | 16 | 11 | 9 |
则下列说法正确的是( )
A.龙岩的该日最高气温最高B.这组数据的众数是16
C.这组数据的中位数是11D.这组数据的平均数是13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店专门销售某种品牌的玩具,成本为30元/件,每天的销售量y(件)与销售单价x(元)之间存在着如图所示的一次函数关系.
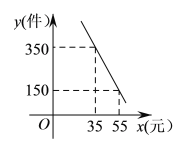
(1)求y与x之间的函数关系式;
(2)当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)为了保证每天的利润不低于3640元,试确定该玩具销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1:y=kx+b与直线l2:y=2x﹣4的交点M的纵坐标为2,且与直线y=﹣x﹣2交x轴于同一点.
(1)求直线l1的表达式;
(2)在给出的平面直角坐标系中作出直线l1的图象,并求出它与直线l2及x轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>0>2x﹣4的解集
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种新产品的成本为30元/件,经市场调查发现,该产品的年销售量y(万件)与销售单价x(元)之间的函数关系如下图:
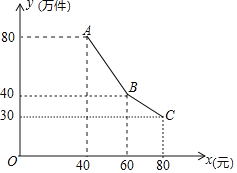
(1)求出y与x之间的函数关系式;
(2)当该产品的售价为多少时,该企业销售该产品获得的年利润最大?最大年利润是多少?(注:年利润=年销售量×(销售单价﹣成本单价))
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
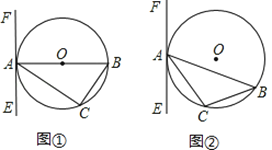
(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
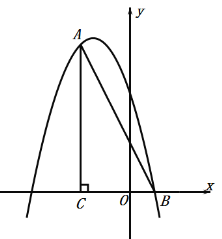
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
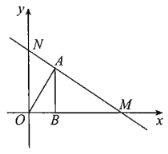
【题目】如图,点M的坐标为![]() ,点A在第一象限,
,点A在第一象限,![]() 轴,垂足为B,
轴,垂足为B,![]() .
.
(1)如果![]() 是等腰三角形,求点A的坐标;
是等腰三角形,求点A的坐标;
(2)设直线MA与y轴交于点N,则是否存在![]() 与
与![]() 相似?若存在,请直接写出点A的坐标;若不存在,请说明理由.
相似?若存在,请直接写出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com