
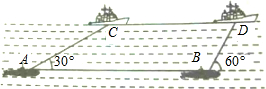
 如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)
如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236) 分析 过C作CE⊥AB于E,过D作DF⊥AB交AB的延长线于F,于是得到CE=DF=600,EF=CD,在Rt△ACE中求得AE=$\frac{CE}{tan30°}$=600$\sqrt{3}$,在RtDBF中,求得BF=$\frac{DF}{tan60°}$=200$\sqrt{3}$,即可得到结论.
解答  解:过C作CE⊥AB于E,过D作DF⊥AB交AB的延长线于F,
解:过C作CE⊥AB于E,过D作DF⊥AB交AB的延长线于F,
则CE=DF=600,EF=CD,
在Rt△ACE中,∵∠A=30°,
∴AE=$\frac{CE}{tan30°}$=600$\sqrt{3}$,
在RtDBF中,∵∠DBF=60°,
∴BF=$\frac{DF}{tan60°}$=200$\sqrt{3}$,
∵AB=300$\sqrt{3}$×20=6000$\sqrt{3}$,
∴CD=EF=5600$\sqrt{3}$,
∴军舰的平均速度=5600$\sqrt{3}$÷20≈48米/分.
点评 此题主要考查了仰角的定义及其解直角三角形的应用,解题时首先正确理解仰角的定义,然后利用三角函数和已知条件构造方程解决问题.


科目:初中数学 来源: 题型:解答题
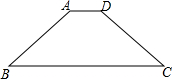 已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.
已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com