
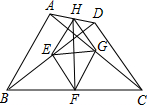
 如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线.E,F,G,H分别是BD,BC,AC,AD的中点.
如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线.E,F,G,H分别是BD,BC,AC,AD的中点.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先根据三角形中位线定理,得出EF=FG=GH=HE,进而得到四边形EFGH是菱形,据此可判断结论是否正确,最后取AB的中点P,连接PE,PG,根据三角形三边关系以及三角形中位线定理,即可得出EG>$\frac{1}{2}$BC-$\frac{1}{2}$AD,即EG>$\frac{1}{2}$(BC-AD).
解答  解:∵E,F分别是BD,BC的中点,
解:∵E,F分别是BD,BC的中点,
∴EF是△BCD的中位线,
∴EF=$\frac{1}{2}$CD,
同理可得,GH=$\frac{1}{2}$CD,FG=$\frac{1}{2}$AB,EH=$\frac{1}{2}$AB,
又∵AB=CD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,故⑤正确,②错误,
∴EG⊥FH,HF平分∠EHG,故①、③正确,
如图所示,取AB的中点P,连接PE,PG,
∵E是BD的中点,G是AC的中点,
∴PE是△ABD的中位线,PG是△ABC的中位线,
∴PE=$\frac{1}{2}$AD,PG=$\frac{1}{2}$BC,PE∥AD,PG∥BC,
∵AD与BC不平行,
∴PE与PG不平行,
∴△PEG中,EG>PG-PE,
∴EG>$\frac{1}{2}$BC-$\frac{1}{2}$AD,即EG>$\frac{1}{2}$(BC-AD),故④错误.
综上所述,正确的有①③⑤.
故选:C.
点评 本题主要考查了中点四边形,三角形三边关系以及三角形中位线定理的运用,解题时注意:三角形的中位线平行于第三边,并且等于第三边的一半.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:选择题
 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
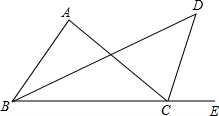 如图,△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.
如图,△ABC中,∠ABC的平分线与∠ACE的平分线相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一个寻宝游戏的寻宝结构是等边三角形ABC及中心O,通道是AB,BC,CA,OA,OB,OC组成.为记录寻宝者的进行路线,将定位仪放置在BC的中点M处,寻宝者的行进路线为B→O→C,若寻宝者匀速行进,设寻宝者行进的时间为x,寻宝者与定位仪之间的距离为y,则y与x的函数关系的图象大致可能为( )
如图,一个寻宝游戏的寻宝结构是等边三角形ABC及中心O,通道是AB,BC,CA,OA,OB,OC组成.为记录寻宝者的进行路线,将定位仪放置在BC的中点M处,寻宝者的行进路线为B→O→C,若寻宝者匀速行进,设寻宝者行进的时间为x,寻宝者与定位仪之间的距离为y,则y与x的函数关系的图象大致可能为( )| A. | 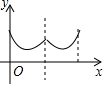 | B. | 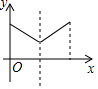 | C. | 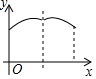 | D. | 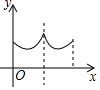 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
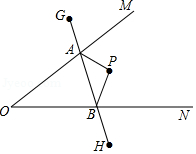 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为14,则△PAB的周长为14.
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为14,则△PAB的周长为14.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com