
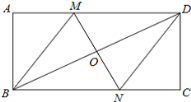
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
【答案】(1)证明见解析;(2)MD长为5.
【解析】
(1)利用矩形性质,证明BMDN是平行四边形,再结合MN⊥BD,证明BMDN是菱形.
(2)利用BMDN是菱形,得BM=DM,设![]() ,则
,则![]() ,在
,在![]() 中使用勾股定理计算即可.
中使用勾股定理计算即可.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵BD的垂直平分线MN
∴BO=DO,
∵在△DMO和△BNO中
∠MDO=∠NBO,BO=DO,∠MOD=∠NOB
∴△DMO ≌ △BNO(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD
∴BMDN是菱形
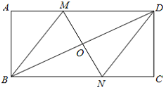
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD=x,则MB=DM=x,AM=(8-x)
在Rt△AMB中,BM2=AM2+AB2
即x2=(8-x)2+42,
解得:x=5
答:MD长为5.


科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
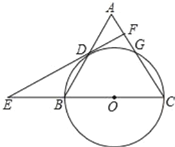
【题目】如图,在![]() ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
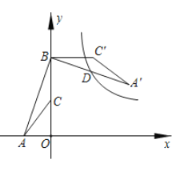
【题目】如图,点A(-2,0), 点B(0,6),C为OB的中点,将![]() 绕点B逆时针旋转90°后得到△A′BC′.若反比例函数
绕点B逆时针旋转90°后得到△A′BC′.若反比例函数![]() 的图象恰好经过A’B的中点D,则k的值为( )
的图象恰好经过A’B的中点D,则k的值为( )
A.12B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
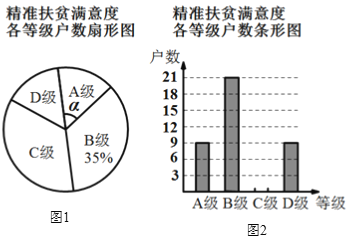
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,他们的形状、大小、质地等完全相同.小兰先从盒子里随机取出一个小球,记下数字为x,放回盒子,摇匀后,再由小田随机取出一个小球,记下数字为y
(1)用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
(2)求小兰、小田各取一次小球所确定的点(x,y)落在反比例函数![]() 的图象上的频率;
的图象上的频率;
(3)求小兰、小田各取一次小球所确定的数x,y满足![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为一幢高3米的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方的点A处建一幢高12米的楼房AB.(设A,C,F在同一水平线上)
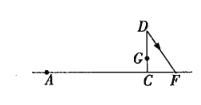
(1)作出楼房AB及它的最大影长AE;
(2)楼房AB建成后,其是否影响温室CD的采光?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
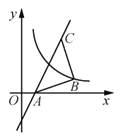
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com