
ЁОЬтФПЁПСЊЯыгыЬНЫїЃК
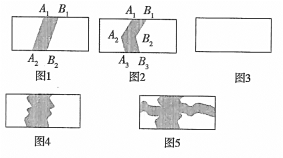
ШчЭМ1,НЋЯпЖЮA1A2БОЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШжСB1B2ЃЌЕУЕНЗтБеЭМаЮA1A2B2B1(МДвѕгАВПЗж)ЃЌдкЭМ2жаЃЌНЋелЯпA1A2A3ЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШжСB1B2B3ЃЌЕУЕНЗтБеЭМаЮA1A2A3B3B2B1(МДвѕгАВПЗж).
(1)дкЭМ3жаЃЌЧыФуРрЫЦЕиЛвЛЬѕгаСНИіелЕуЕФелЯпЃЌЭЌбљЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌДгЖјЕУЕНвЛИіЗтБеЭМаЮЃЌВЂгУвѕгАБэЪОЃЛ
(2)ЧыФуЗжБ№аДГіЩЯЪіШ§ИіЭМаЮжаГ§ШЅвѕгАВПЗжКѓЪЃгрВПЗжЕФУцЛ§(ЩшГЄЗНаЮЫЎЦНЗНЯђГЄОљЮЊa,ЪњжБЗНЯђГЄОљЮЊb) ЃКS1= ЃЌS2= ЃЌS3= ;
(3)ШчЭМ4ЃЌдквЛПщГЄЗНаЮВнЕиЩЯЃЌгавЛЬѕЭфЧњЕФаЁТЗ(аЁТЗШЮКЮЕиЗНЕФЫЎЦНПэЖШЖМЪЧ2ИіЕЅЮЛГЄЖШЃЌГЄЗНаЮЫЎЦНЗНЯђГЄЮЊa,ЪњжБЗНЯђГЄЮЊb)ЃЌдђПеАзВПЗжБэЪОЕФВнЕиУцЛ§ЪЧЖрЩйЃП
(4)ШчЭМ5ЃЌШєдк(3)жаЕФВнЕиЩЯгжгавЛЬѕКсЯђЕФЧњаЁТЗ(аЁТЗШЮКЮЕиЗНЕФПэЖШЖМЪЧ1ИіЕЅЮЛГЄЖШЃЉЃЌдђПеАзВПЗжБэЪОЕФВнЕиУцЛ§ЪЧЖрЩйЃП
ЁОД№АИЁП (1)МћНтЮіЃЛ(2)a(b-1)ЃЌa(b-1)ЃЌa(b-1)ЃЛ(3) b(a-2)ЃЛ(4)ЃЈa-2)(b-1)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌжБНгЛЭММДПЩЃЌзЂвтД№АИВЛЮЈвЛЃЌжЛвЊЛвЛЬѕгаСНИіелЕуЕФелЯпЃЌЕУЕНвЛИіЗтБеЭМаЮМДПЩЃЎ
ЃЈ2ЃЉНсКЯЭМаЮЃЌИљОнЦНвЦЕФаджЪПЩжЊЃЌЭМ1ЭМ2ЭМ3жаПеАзВПЗжЕФУцЛ§ЖМПЩПДзїЪЧвдaЉ1ЮЊГЄЃЌbЮЊПэЕФГЄЗНаЮЕФУцЛ§ЃЎ
ЃЈ3ЃЉНсКЯЭМаЮЃЌЭЈЙ§ЦНвЦЃЌПеАзВПЗжПЩЦНвЦЮЊвдaЉ2УзЮЊГЄЃЌbУзЮЊПэЕФГЄЗНаЮЃЌИљОнГЄЗНаЮЕФУцЛ§ПЩЕУВнЕиВПЗжЫљеМЕФУцЛ§ЃЎ
ЃЈ4ЃЉНсКЯЭМаЮПЩжЊЃЌПеАзВПЗжЫљеМЕФУцЛ§=ЃЈaЉ2ЃЉУзЮЊГЄЃЌ(bЉ1)УзЮЊПэЕФГЄЗНаЮЕФУцЛ§ЃЎ
ЃЈ1ЃЉЛЭМШчЯТЃК

ЃЈ2ЃЉS1=abЉbЃЌS=abЉbЃЌS2=abЉbЃЌS3=abЉb
РэгЩЃК1ЃЎНЋЁАаЁТЗЁБбизХзѓгвСНИіБпНчЁАМєШЅЁБЃЛ2ЃЎНЋзѓВрЕФВнЕиЯђгвЦНвЦвЛИіЕЅЮЛЃЛ3ЃЎЕУЕНвЛИіаТЕФОиаЮЃЎдкаТЕУЕНЕФОиаЮжаЃЌЦфзнЯђПэШдШЛЪЧbЃЎЦфЫЎЦНЗНЯђЕФГЄБфГЩСЫaЉ1ЃЌЫљвдВнЕиЕФУцЛ§ОЭЪЧЃКbЃЈaЉ1ЃЉ=abЉbЃЎ
ЃЈ3ЃЉЁпзнЯђаЁТЗШЮКЮЕиЗНЕФЫЎЦНПэЖШЖМЪЧ2ИіЕЅЮЛЃЌЁрПеАзВПЗжБэЪОЕФВнЕиУцЛ§ЪЧЃЈaЉ2ЃЉbЃЛ
ЃЈ4ЃЉЁпзнЯђаЁТЗШЮКЮЕиЗНЕФЫЎЦНПэЖШЖМЪЧ2ИіЕЅЮЛЃЌКсЯђаЁТЗШЮКЮЕиЗНЕФПэЖШЖМЪЧ1ИіЕЅЮЛЃЌЁрПеАзВПЗжБэЪОЕФВнЕиУцЛ§ЪЧЃЈaЉ2)(bЉ1)ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
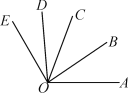
ЁОЬтФПЁПШчЭМЃЌOBЪЧЁЯAOCЕФЦНЗжЯпЃЌODЪЧЁЯCOEЕФЦНЗжЯпЃЎ
(1)ШчЙћЁЯAOCЃН70ЁуЃЌЁЯCOEЃН50ЁуЃЌФЧУДЁЯBODЪЧЖрЩйЖШЃП
(2)ШчЙћЁЯBODЃН70ЁуЃЌФЧУДЁЯAOEЪЧЖрЩйЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКХзЮяЯпy=ax2+bx+cНЛyжсгкЕуCЃЈ0ЃЌ4ЃЉЃЌЖдГЦжсx=2гыxжсНЛгкЕуDЃЌЖЅЕуЮЊMЃЌЧвDM=OC+ODЃЌ 
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуPЃЈxЃЌyЃЉЪЧЕквЛЯѓЯоФкИУХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁїPCDЕФУцЛ§ЮЊSЃЌЧѓSЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЌВЂЧѓЕБxШЁЖрЩйЪБЃЌSЕФжЕзюДѓЃЌзюДѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy= ![]() x+4гыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЌЕуCЁЂDЗжБ№ЮЊЯпЖЮABЁЂOBЕФжаЕуЃЌЕуPЮЊOAЩЯвЛЖЏЕуЃЌPC+PDжЕзюаЁЪБЕуPЕФзјБъЮЊЃЈ ЃЉ
x+4гыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЌЕуCЁЂDЗжБ№ЮЊЯпЖЮABЁЂOBЕФжаЕуЃЌЕуPЮЊOAЩЯвЛЖЏЕуЃЌPC+PDжЕзюаЁЪБЕуPЕФзјБъЮЊЃЈ ЃЉ
A.ЃЈЉ3ЃЌ0ЃЉ
B.ЃЈЉ6ЃЌ0ЃЉ
C.ЃЈЉ ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
D.ЃЈЉ ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчзгдЊМўГЇзМБИЩњВњ1200ИіЕчзгдЊМўЃЌЩњВњвЛАыКѓЃЌгЩгквЊОЁПьЭЖШыЪаГЁЃЌИУГЇЬсИпСЫЩњВњаЇТЪЃЌУПЬьЩњВњЕФЕчзгдЊМўИіЪ§ЪЧдРДЕФ1.2БЖЃЌНсЙћЬсЧА2ЬьЭъГЩСЫШЮЮёЃЌЧѓИУГЇКѓРДУПЬьЩњВњЕчзгдЊМўЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
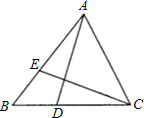
ЁОЬтФПЁПШчЭМЃЌЁїABCжаBA=BCЃЌЕуDЪЧABбгГЄЯпЩЯвЛЕуЃЌDFЁЭACгкFНЛBCгкEЃЌ
ЧѓжЄЃКЁїDBEЪЧЕШбќШ§НЧаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊOAЁЭOBЃЌЁЯAOD=ЁЯBOCгЩДЫХаЖЈOCЁЭODЃЌЯТУцЪЧЭЦРэЙ§ГЬЃЌЧыЬюПе.

НтЃКЁпOAЁЭOB(вбжЊ)
Ыљвд_____=90ЁуЃЈ________ЃЉ
вђЮЊ_____=ЁЯAOD-ЁЯAOCЃЌ____=ЁЯBOC-ЁЯAOCЃЌЁЯAOD=ЁЯBOCЃЌ
Ыљвд______=_____(ЕШСПДњЛЛ)
Ыљвд______=90Ёу
ЫљвдOCЁЭOD.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЕуDдкBCЩЯЃЌЕуEдкABЩЯЃЌBD=BEЃЌвЊЪЙЁїADBЁеЁїCEBЃЌЛЙашЬэМгвЛИіЬѕМўЃЎ
(1)ИјГіЯТСаЫФИіЬѕМўЃКЂйAD=CE ЂкAE=CD ЂлЁЯBAC=ЁЯBCA ЂмЁЯADB=ЁЯCEBЧыФуДгжабЁГівЛИіФмЪЙЁїADBЁеЁїCEBЕФЬѕМўЃЌВЂИјГіжЄУїЃЛ
ФубЁГіЕФЬѕМўЪЧ
жЄУїЃК
(2)дк(1)жаЫљИјГіЕФЬѕМўжаЃЌФмЪЙЁїADBЁеЁїCEBЕФЛЙгаФФаЉЃПжБНгдкЬтКѓКсЯпЩЯаДГіТњзуЬтвтЕФЬѕМўађКХЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
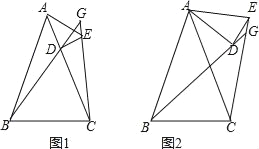
ЁОЬтФПЁПвбжЊAB=ACЃЌAD=AEЃЌЁЯBAC=ЁЯDAEЃЌжБЯпBDЁЂCEНЛгкЕуGЃЌ
ЃЈ1ЃЉШчЭМ1ЃЌЕуDдкACЩЯЃЌЧѓжЄЃКЁЯBGC=ЁЯBACЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDВЛдкACЩЯЃЌЃЈ1ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com