
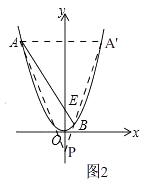
����Ŀ����ͼ1������ԭ���������y=ax2+bx+c��x�����һ������Ϊ��C����˫����y= ![]() �ཻ�ڵ�A��B��ֱ��AB��ֱ���x�ᡢy�ύ�ڵ�D��E����֪��A������Ϊ����1��4������B�ڵ����������ҵ�x�ᡢy��ľ�����ȣ�
�ཻ�ڵ�A��B��ֱ��AB��ֱ���x�ᡢy�ύ�ڵ�D��E����֪��A������Ϊ����1��4������B�ڵ����������ҵ�x�ᡢy��ľ�����ȣ�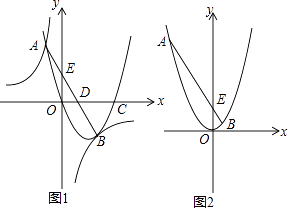
��1����˫���ߺ������ߵĽ���ʽ��
��2�������ABC�������
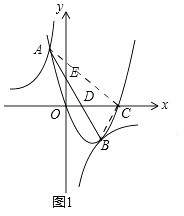
��3����ͼ2����������ƽ����������ԭ����ʱ��ֱ��AB��֮ƽ�ƣ����жϣ���y��ĸ��������Ƿ���ڵ�P��ʹ��PAB������Բ��Բ����y���ϣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺�ѵ�A���������˫���ߵĽ���ʽ�ã�k=��1��4=��4��
����˫���ߵĽ���ʽΪy=�� ![]() ��
��
���B��������m����m����
�ߵ�B��˫�����ϣ�
�ੁm2=��4�����m=2��m=��2��
�ߵ�B�ڵ������ޣ�
��m=2��
��B��2����2����
����A��B��C���������ã� 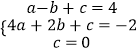 ��
��
��ã� 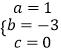 ��
��
�������ߵĽ���ʽΪy=x2��3x��
��2���⣺��ͼ1������AC��BC��
��y=0����x2��3x=0��
��x=0��x=3��
��C��3��0����
��A����1��4����B��2����2����
��ֱ��AB�Ľ���ʽΪy=��2x+2��
�ߵ�D��ֱ��AB��x��Ľ��㣬
��D��1��0����
��S��ABC=S��ADC+S��BDC= ![]() ��2��4+
��2��4+ ![]() ��2��2=6��
��2��2=6��
��3���⣺���ڣ����ɣ���ͼ2��
��ԭ�����ߵĽ���ʽΪy=x2��3x=��x�� ![]() ��2��
��2�� ![]() ��
��
��ԭ�����ߵĶ�������Ϊ�� ![]() ����
���� ![]() ����
����
������������ƽ�� ![]() ����λ��������ƽ��
����λ��������ƽ�� ![]() ����λ��
�����
��ƽ��ǰA����1��4����B��2����2����
��ƽ�ƺ��A���� ![]() ��
�� ![]() ����B��
����B�� ![]() ��
�� ![]() ����
����
���A����y��ĶԳƵ�A'�� ![]() ��
�� ![]() ����
����
����A'B���ӳ���y���ڵ�P������AP��
�ɶԳ���֪����APE=��BPE��
���APB������Բ��Բ����y���ϣ�
��B�� ![]() ��
�� ![]() ����A'��
����A'�� ![]() ��
�� ![]() ����
����
��ֱ��A'B�Ľ���ʽΪy=3x�� ![]() ��
��
��P��0���� ![]() ����
����
����������1�����Ƚ���A��������뷴���������Ľ���ʽ���k��ֵ��Ȼ�������B��ֵ�������ݵ�A���������˫���ߵĽ���ʽ�������ó���B�����꣬�����A��B��O�����������������ߵĽ���ʽ�����a��b��c��ֵ���ɣ�
��2���ɵ�A�͵�B����������ֱ��AB�Ľ���ʽ��Ȼ��y=0����õ�D�ĺ����꣬����������ε��������⼴�ɣ�
��3����ȷ����ƽ�ƺ��A��B�����꣬���������A����y��ĶԳƵ�����꣬���ֱ��BA'�Ľ���ʽ���ɵó���P������.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�羰����Ʊ�۸���ͼ��ʾ���ƸԳ�����ι�˾�мס������������Ŷӣ��ƻ��ڡ���һ��С�ƽ����ڼ䵽�þ������森���Ŷ��ο�����֮��Ϊ120�ˣ����Ŷ�����������50�ˣ�����Ŷ�����Ϊx�ˣ�����ס������Ŷӷֱ�����Ʊ�����Ŷ���Ʊ��֮��ΪWԪ��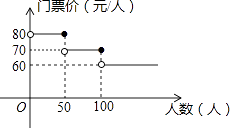
��1����W����x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�������Ŷ�����������100�ˣ���˵���ס������Ŷ����Ϲ�Ʊ�ȷֱ�Ʊ���ɿɽ�Լ����Ǯ��
��3������һ��С�ƽ���֮�÷羰������Ʊ�۸��������µ���������������50��ʱ����Ʊ�۸䣻��������50�˵�������100��ʱ��ÿ����Ʊ����aԪ����������100��ʱ��ÿ����Ʊ����2aԪ���ڣ�2���������£����ס������������Ŷӡ���һ��С�ƽ���֮��ȥ���棬�������Ŷ����Ϲ�Ʊ�ȷֱ�Ʊ����Լ3400Ԫ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��Լˮ��Դ���ƶ����µľ�����ˮ�շѱ��������±����û�ÿ�½��ɵ�ˮ��y��Ԫ����ÿ����ˮ��x��m3��֮��Ĺ�ϵ��ͼ��ʾ��
��1����y����x�ĺ�������ʽ��
��2����ij�û��������·ݹ���ˮ40m3�����·���ˮ��������25m3��������ˮ��79.8Ԫ������û��������·ݵ���ˮ�����Ƕ���m3��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����ABCD����A��B��y�ᡢx���ϣ���B��x�����˶�ʱ��A��֮��y���˶�������ABCD����״���ֲ��䣬����AB��2��BC��1���˶������У���D����O��������Ϊ__________��
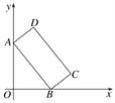
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ѿ���Ϊ�����ձ��ע�Ļ��⣬����������Ӱ�����ǵij��У���Ӱ�������ǵĽ�������2017��2����ĩ��Ϣ�ڼ䣬ijУ���꼶һ���ۺ�ʵ��С���ͬѧ�ԡ�������������Ҫ����Ϊ���⣬���������̫ԭ�в�������Ĺ۵㣬���Ե��������������������������²�������ͳ�Ʊ���ͳ��ͼ���۲첢�ش��������⣺
��� | ������������Ҫ���� | �ٷֱ� |
A | ��ҵ��Ⱦ | 45% |
B | ����β���ŷ� | m |
C | ���д�ȼú���� | 15% |
D | �������̻�����ȣ� | n |
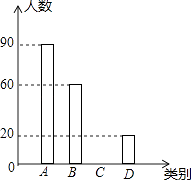
��1������������α����������������m��n��ֵ������ȫ����ͳ��ͼ��
��2����������800���˿ڣ�������Ƴ���B��C������������ж����ˣ�
��3��С��ͬѧ���ĸ��ʵء���С����״����ȫ��ͬ��С���ϱ��A��B��C��D�����ĸ�������������Ҫ�����У�����һ�������ĺ����У����������ȡһ��С�Ż�ȥ���������ȡһ��С�����û���״ͼ���б��ķ��������Сӱͬѧ�պó鵽B��D�ĸ��ʣ�����A��B��C��D��ʾ����Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
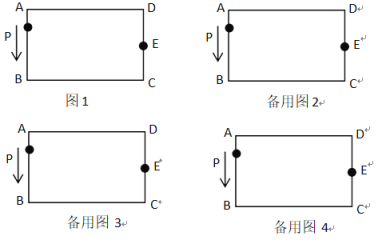
����Ŀ����ͼ��������ABCD��AB=CD=4��BC=AD=8����A����B����C����D��90�㣬EΪCD�ߵ��е㣬PΪ������ABCD���ϵĶ��㣬����P��A����������A B C E�˶���E��ֹͣ�����P������·��Ϊ![]() ��APE�����Ϊ
��APE�����Ϊ![]() .
.
��1����![]() ʱ����ͼ1�л�����ͼ���������Ӧ
ʱ����ͼ1�л�����ͼ���������Ӧ![]() ��ֵ��
��ֵ��
��2�����ñ���ͼ������ͼ��д��![]() ��
��![]() ֮��Ĺ�ϵʽ.
֮��Ĺ�ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
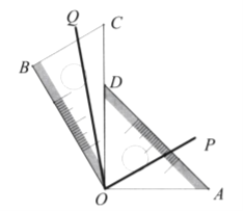
����Ŀ��һ�����ǰ壬![]()
��1������ͼ����ʾ��ʽ���ã���![]() ���㹲�ߣ�
���㹲�ߣ�![]() ����
����![]() �Ķ�����
�Ķ�����
��2���ڣ�1���������£���![]() �ֱ���
�ֱ���![]() ��
��![]() �ڲ���һ�����ߣ���
�ڲ���һ�����ߣ���![]() ���Ե�
���Ե�![]() Ϊ���ģ��ֱ��
Ϊ���ģ��ֱ��![]() λ�ó�������
λ�ó�������![]() ��/�롢
��/�롢![]() ��/�����ת�ٶ�����ʱ�뷽����ת����
��/�����ת�ٶ�����ʱ�뷽����ת����![]() ��
��![]() �ص�ʱ��������ת��ֹͣ����˵��:����ת
�ص�ʱ��������ת��ֹͣ����˵��:����ת![]() ���
���![]()
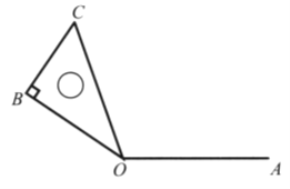
��3�������ǰ�![]() (����
(����![]() ��)��һ��DZ����ǰ壬����ͼ����ʾ��ʽ���ã�ʹ
��)��һ��DZ����ǰ壬����ͼ����ʾ��ʽ���ã�ʹ![]() ��������
��������![]() ����
����![]() ����
����![]() ��
��![]() �Ķ���֮�ȣ�
�Ķ���֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ������ѧ�Ļ��е�һ��屦������ͼ���У��Ȳ������ĶԳ�ͼ��Ҳ������Գ�ͼ�ε��ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ��ABΪֱ������BAC��ƽ���߽���O�ڵ�D������D��ֱ�߷ֱ�AB��AC���ӳ����ڵ�E��F��AF��EF�� 
��1����֤��EF�ǡ�O�����ߣ�
��2��Сǿͬѧͨ��̽�����֣�AF+CF=2AO���������Сǿͬѧ֤����һ���ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com