练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

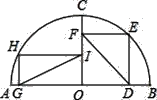
    【题目】如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I，F在OC上，点H，E在半圆上，可证：IG=FD．小云发现连接图中已知点得到两条线段，便可证明IG=FD．

    请回答：小云所作的两条线段分别是_____和_____；

    证明IG=FD的依据是矩形的对角线相等，_____和等量代换．

    【答案】OH OE 同圆的半径相等

    【解析】

    连接OH、OE，由矩形OGHI和正方形ODEF的性质得出IG=OH，OE=FD，由OH=OE，即可得出结论．

    解：

    连接OH、OE，如图所示：

    ∵在矩形OGHI和正方形ODEF中，IG=OH，OE=FD，

    ∵OH=OE，

    ∴IG=FD；

    故答案为：OH、OE，同圆的半径相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，点B（0，3），点C（4，0）

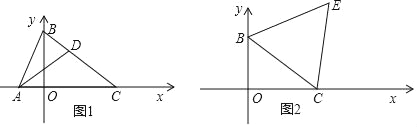
    （1）求线段BC的长．

    （2）如图1，点A（﹣1，0），D是线段BC上的一点，若△BAD∽△BCA时，求点D的坐标．

    （3）如图2，以BC为边在第一象限内作等边△BCE，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数（a＜0）图象与x轴的交点A、B的横坐标分别为﹣3，1，与y轴交于点C，下面四个结论：

    ①16a﹣4b+c＜0；②若P（﹣5，y1），Q（，y2）是函数图象上的两点，则y1＞y2；③a=﹣c；④若△ABC是等腰三角形，则b=﹣．其中正确的有______（请将结论正确的序号全部填上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

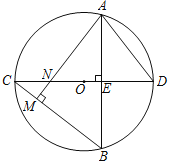
    【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.

    (1)求证:AD=AN;

    (2)若AB=8,ON=1,求⊙O的半径.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在△ABC中，∠A=90°，AB=AC，点D为BC的中点．

    （1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE=AF；

    （2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE=AF吗？请利用图②说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

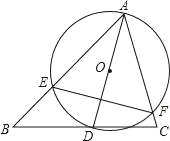
    【题目】如图，△ABC中，∠BAC＝60°，∠ABC＝45°，AB＝4，D是线段BC上的一个动点，以AD为直径作⊙O分别交AB、AC于E、F，连结EF，则线段EF长度的最小值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）已知⊙O的直径为10cm，点A为⊙O外一定点，OA=12cm，点P为⊙O上一动点，求PA的最大值和最小值．

    （2）如图：=，D、E分别是半径OA和OB的中点．求证：CD=CE．

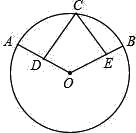
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店经销一种成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克．若销售价每涨1元，则月销售量减少10千克．

    （1）要使月销售利润达到最大，销售单价应定为多少元？

    （2）要使月销售利润不低于8000元，请结合图象说明销售单价应如何定？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在菱形 ABCD 中，对角线 AC、BD 相交于 O，如果菱形 ABCD 的周长为 20，BD=6，则下列结论中， 正确的是（ 　 ）

    A.AC=8B.AC=4

    C.菱形 ABCD 的面积为 48D.菱形ABCD 的高为 9.6

    查看答案和解析>>

    同步练习册答案