
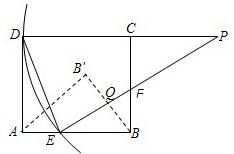
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.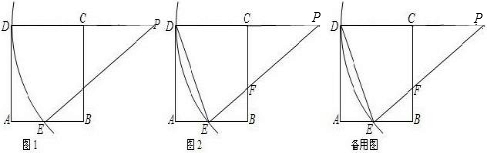
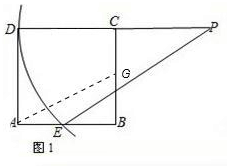
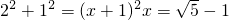 (负数舍去).
(负数舍去).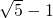 .
.
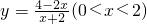 ;
;
 ,
,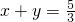 ,
,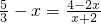 ,
,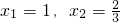 .
.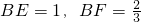 ;
; ,BB'=
,BB'= .
.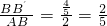 ,
,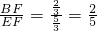 ,
,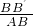 =
=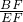 ,
,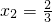 时,
时,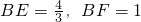 .
.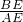 =
=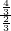 =2,
=2,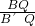 =1,
=1, ,AE=1时,△AB'B∽△BEF;
,AE=1时,△AB'B∽△BEF; ,
,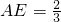 时,△AB'B与△BEF不相似.
时,△AB'B与△BEF不相似. BC,进而可在Rt△ABG中,由勾股定理求得AE的长.
BC,进而可在Rt△ABG中,由勾股定理求得AE的长. 时,x+y=
时,x+y= ,联立(2)的函数关系式可求得此时x的值,进而可求出AE、BF的长;根据折叠的性质知:EF垂直平分BB′,设垂足为Q;在Rt△BEF中,根据直角三角形面积的不同表示方法,可求得BQ的长,也就得出了BB′的长;然后再判断两个直角三角形的对应边是否成比例即可.
,联立(2)的函数关系式可求得此时x的值,进而可求出AE、BF的长;根据折叠的性质知:EF垂直平分BB′,设垂足为Q;在Rt△BEF中,根据直角三角形面积的不同表示方法,可求得BQ的长,也就得出了BB′的长;然后再判断两个直角三角形的对应边是否成比例即可.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
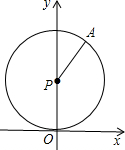 已知:如图,⊙P与x轴切于点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为
已知:如图,⊙P与x轴切于点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 4 |
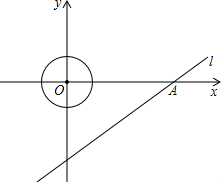 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?查看答案和解析>>
科目:初中数学 来源: 题型:
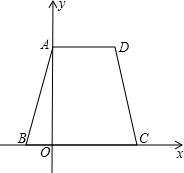 B=2
B=2| 10 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
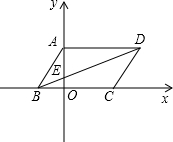 点E,AB=
点E,AB=| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
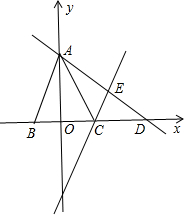 将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D.
将△AOC沿直线AC折叠,点O落在平面内的点E处,直线AE交x轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com