
【题目】如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,对于下列结论:①△ABE≌△CDF;②AM=MN=NC;③EM=![]() BM,④S△ABM=S△AME,其中正确的有( )
BM,④S△ABM=S△AME,其中正确的有( )
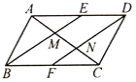
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①已知四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠DAB=∠DCB,已知E、F分别是边AD、BC的中点,可得AE=![]() AD=CF=
AD=CF=![]() BC,可证得△ABE≌△CDF
BC,可证得△ABE≌△CDF
②证明△ABM≌△CDN,得到AM=CN,再证明BE∥DF,F分别是边BC的中点,可得CN=MN,即可得出AM=CN=MN
③证明ME=![]() ND,因为△ABM≌△CDN,可得BM=DN,ME=
ND,因为△ABM≌△CDN,可得BM=DN,ME=![]() BM,可判断③
BM,可判断③
④在求△ABM和△AME面积时,有同一个高,它们的底分别为BM,ME,比较底边大小即可求解.
①∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠DAB=∠DCB
∵E、F分别是边AD、BC的中点
∴AE=![]() AD=CF=
AD=CF=![]() BC
BC
∴△ABE≌△CDF
故①正确
②∵△ABE≌△CDF
∴∠ABM=∠NDC
∵四边形ABCD是平行四边形,AB∥CD
∴∠BAM=∠NCD,AB=CD
∴△ABM≌△CDN
∴AM=CN,
∵∠AEB=∠DFC
∵AD∥BC
∴∠AEB=∠EBC
∴∠DFC=∠EBC
∴BE∥DF
∵F是边BC的中点
∴CN=MN
即AM=CN=MN
故②正确
③∵BE∥DF,E是边AD的中点
∴M是边AN的中点,即ME是△AND的中位线
∴ME=![]() ND
ND
∵△ABM≌△CDN
∴BM=DN
∴ME=![]() BM
BM
故③正确
④过点A作AH⊥BE于H,如图所示
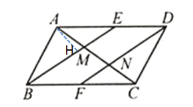
在求△ABM和△AME面积时,有同一个高AH,它们的底分别为BM,ME,
∵EM=![]() BM ,
BM ,
∴S△ABM>S△AME
故④错误
综上所述①②③正确
故选:C


科目:初中数学 来源: 题型:
【题目】我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
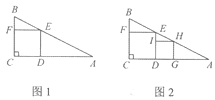
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好的决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
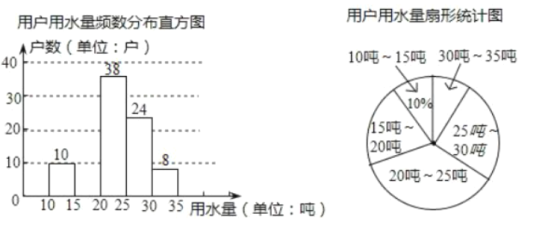
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“![]() 吨—
吨—![]() 吨”部分的圆心角的度数.
吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户![]() 吨,那么该地区
吨,那么该地区![]() 万用户中约有多少用户的用水全部享受基本价格?
万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)经过几秒△PCQ的面积为△ACB的面积的![]() ?
?
(2)经过几秒,△PCQ与△ACB相似?
(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
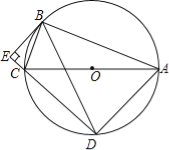
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
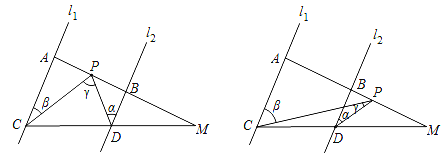
【题目】如图,已知l1∥l2,线段MA分别与直线l1,l2交于点A,B,线段MC分别与直线l1,l2交于点C,D,点P在线段AM上运动(P点与A,B,M三点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)若点P在A,B两点之间运动时,若a=25°,β=40°,那么γ= .
(2)若点P在A,B两点之间运动时,探究α,β,γ之间的数量关系,请说明理由;
(3)若点P在B,M两点之间运动时,α,β,γ之间有何数量关系?(只需直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季是垂钓的好季节.一天甲、乙两人到松花江的![]() 处钓鱼,突然发现在
处钓鱼,突然发现在![]() 处有一人不慎落入江中呼喊救命.如图,在
处有一人不慎落入江中呼喊救命.如图,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从
方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从![]() 处跳水游向
处跳水游向![]() 处救人;此时乙从
处救人;此时乙从![]() 沿岸边往正东方向奔跑40米到达
沿岸边往正东方向奔跑40米到达![]() 处,再从
处,再从![]() 处下水游向
处下水游向![]() 处救人,已知
处救人,已知![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
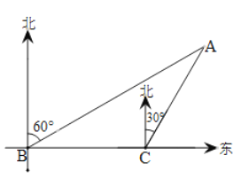
(1)求![]() 、
、![]() 的长.
的长.
(2)试问甲、乙二人谁能先救到人,请通过计算说明理由.(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福州电信公司开设了A、B两种市内移动通信业务:A种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.1元;B种使用者不缴月租费,每通话1分钟,付话费0.3元.若一个月内通话时间为x分钟,A、B两种的费用分别为![]() 和
和![]() 元.
元.
(1)试分别写出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(2)每月通话时间为多长时,开通A种业务和B种业务费用一样.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com