
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 . (请写出正确结论的序号).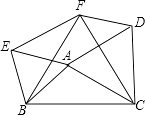
【答案】①②
【解析】解:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
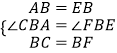 ,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形,选项②正确;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
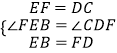 .
.
∴△FEB≌△CDF(SAS),选项①正确;
若AB=AC,∠BAC=120°,则有AE=AD,∠EAD=120°,此时AEFD为菱形,选项③错误,
所以答案是:①②.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形)的相关知识才是答题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能够成等边三角形,那么平移的距离为( )
A.1个单位
B.![]() 个单位
个单位
C.![]() 个单位
个单位
D.![]() 个单位
个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
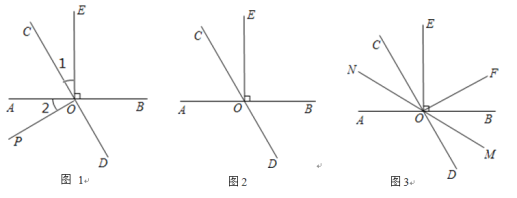
【题目】已知:直线 AB与直线 CD交于点 O,过点 O作 OE⊥AB.
①如图 1,OP 为∠AOD 内的一条射线,若∠1=∠2,求证:OP⊥CD;
②如图 2,若∠BOC=2∠AOC,求∠COE 的度数;
③如图 3.在(2)的条件下,过点 O 作 OF⊥CD,经过点 O 画直线 MN,若射线 OM平分∠BOD,请直接写出图中与 2∠EOF 度数相等的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于![]() ,
,![]() 交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点
交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点![]() (如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.
(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.
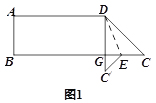
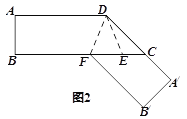
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1 ,
其中正确的是( )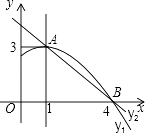
A.①②③
B.①③④
C.①③⑤
D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点O在△ABC的内部,∠BOC=90°,OB=OC,D,E,F,G分别是AB,OB,OC,AC的中点.
(1)求证:四边形DEFG是矩形;
(2)若DE=2,EF=3,求△ABC的面积.
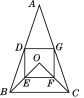
查看答案和解析>>
科目:初中数学 来源: 题型:
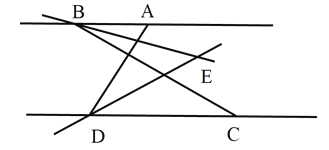
【题目】AB∥CD,C在 D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点 E.∠ADC=70°.
(1)求∠EDC 的度数;
(2)若∠ABC=30°,求∠BED 的度数;
(3)将线段 BC沿 DC方向移动,使得点 B在点 A的右侧,其他条件不变,若∠ABC=n°,请直接写出∠BED 的度数(用含 n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则矩形ABCD的面积是( )
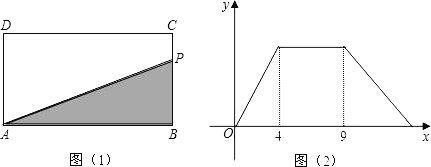
A. 10B. 16C. 20D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com