
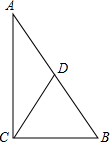
 请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,并进行证明:
请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,并进行证明: 解:逆命题是:如果一个三角形一边上的中线等于这边的一半,那么这个三角是直角三角形.
解:逆命题是:如果一个三角形一边上的中线等于这边的一半,那么这个三角是直角三角形.| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 点A(0,2),点C(-1,0),如图所示:抛物线y=2ax2+ax-
点A(0,2),点C(-1,0),如图所示:抛物线y=2ax2+ax-| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
 限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.
限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,将一块腰长为
如图,在平面直角坐标系中,将一块腰长为| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的等腰直角三角板ABC放在第二象
的等腰直角三角板ABC放在第二象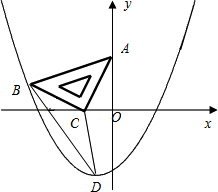 限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.
限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.查看答案和解析>>
科目:初中数学 来源:2012届浙江省慈溪市金山中学九年级学业模拟考试数学卷(带解析) 题型:解答题
如图,在平面直角坐标系中,将一块腰长为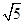 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(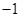 ,0),点B在抛物线
,0),点B在抛物线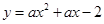 上.
上.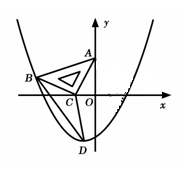
(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的解析式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com