
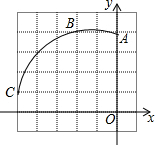
 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:分析 (1)根据线段垂直平分线性质找出D即可;
(2)根据勾股定理即可求出CD,证△CED≌△DOA,根据全等三角形的性质求出∠COE=∠OAD,根据三角形内角和定理即可求出∠ADC;
(3)根据弧长公式求出弧长,根据圆的周长公式求出即可.
解答 解:(1)如图:
D的坐标为(-1,0),
故答案为:(-1,0);
(2)如图:
设小正方形的边长为1,由勾股定理得:CD=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
在△CED和△DOA中
$\left\{\begin{array}{l}{CE=DO}\\{∠CEO=∠DOA=90°}\\{OE=OA}\end{array}\right.$
∴△CED≌△DOA,
∴∠COE=∠OAD,
∵∠AOD=90°,
∴∠OAD+∠ADO=90°,
∴∠ADC=180°-(∠CDE+∠ADO)=180°-(∠OAD+∠ADO)=180°-90°=90°,
故答案为:$\sqrt{17}$,90°;
(3)$\widehat{AC}$的长为$\frac{90π×\sqrt{17}}{180}$═$\frac{\sqrt{17}}{2}$π,
设圆锥底面半径为r,
则2πr=$\frac{\sqrt{17}}{2}$π,
解得:r=$\frac{\sqrt{17}}{4}$.
故答案为:$\frac{\sqrt{17}}{4}$.
点评 此题主要考查了弧长公式,勾股定理,全等三角形的性质和判定,三角形内角和定理的应用,能正确运用定理进行推理和计算是解此题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:在梯形ABCD中两条对角线AC、BD相交于点O,已知OB=18cm,OD=12cm,则S△ABD:S△ABC=$\frac{2}{3}$.
如图:在梯形ABCD中两条对角线AC、BD相交于点O,已知OB=18cm,OD=12cm,则S△ABD:S△ABC=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
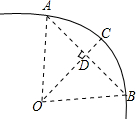 如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )
如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )| A. | 60m | B. | 80m | C. | 100m | D. | 120m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
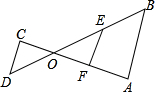 如图,若DC∥FE∥AB,则有( )
如图,若DC∥FE∥AB,则有( )| A. | $\frac{OD}{OF}$=$\frac{OC}{OE}$ | B. | $\frac{OF}{OB}$=$\frac{OA}{OC}$ | C. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | D. | $\frac{CD}{EF}$=$\frac{OD}{OE}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com