
【题目】湖州某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 15 | 12 |
月污水处理能力(吨/月) | 250 | 200 |
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
【答案】(1)有3种购买方案:第一种是购买3台A型污水处理设备,7台B型污水处理设备;第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备;(2)购买3台A型污水处理设备,7台B型污水处理设备更省钱.
【解析】
(1)设购买A型号的污水处理设备x台,则购买B型号的污水处理设备(10-x)台,根据购买资金不超过136万元及月处理污水能力不低于2150吨,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再由x为整数即可得出各购买方案;
(2)根据总价=单价×数量,分别求出3种购买方案所需总费用,比较后即可得出结论.
(1)设购买![]() 型号的污水处理设备
型号的污水处理设备![]() 台,则购买
台,则购买![]() 型号的污水处理设备
型号的污水处理设备![]() 台,
台,
根据题意得:![]()
解得:![]()
∵![]() 是整数
是整数
∴![]() 或
或![]() 或
或![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
答:有3种购买方案:第一种是购买3台A型污水处理设备,7台B型污水处理设备;第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备.
(2)当![]() 时,购买资金为15×3+12×7=129(万元),
时,购买资金为15×3+12×7=129(万元),
当![]() 时,购买资金为15×4+12×6=132(万元),
时,购买资金为15×4+12×6=132(万元),
当![]() 时,购买资金为15×5+12×5=135(万元).
时,购买资金为15×5+12×5=135(万元).
∵135>132>129,
∴为了节约资金,应购污水处理设备A型号3台,B型号7台.
答:购买3台A型污水处理设备,7台B型污水处理设备更省钱


科目:初中数学 来源: 题型:
【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号 | 月租费(元) | 免费时间(分) | 超过免费时间的通话费(元/分) |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四根长度一定的木条,其中AB=6cm,CD=15cm,将这四根木条用小钉绞合在一起,构成一个四边形ABCD(在A、B、C、D四点处是可以活动的).现固定AB边不动,转动这个四边形,使它的形状改变,在转动的过程中有以下两个特殊位置.
位置一:当点D在BA的延长线上时,点C在线段AD上(如图2);
位置二:当点C在AB的延长线上时,∠C=90°.
(1)在图2中,若设BC的长为![]() ,请用含
,请用含![]() 的代数式表示AD的长;
的代数式表示AD的长;
(2)在图3中画出位置二的示意图
(3)利用图2、图3求图1的四边形ABCD中BC、AD边的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC=45°,D是BC边上的一点,BD=2,将△ACD沿直线AD翻折,点C刚好落在AB边上的点E处.若P是直线AD上的动点,则△PEB的周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
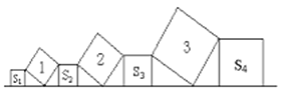
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3a(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,2),连接BC.
(1)求该抛物线的解析式和对称轴,并写出线段BC的中点坐标;
(2)将线段BC先向左平移2个单位长度,再向下平移m个单位长度,使点C的对应点C1恰好落在该抛物线上,求此时点C1的坐标和m的值;
(3)若点P是该抛物线上的动点,点Q是该抛物线对称轴上的动点,当以P,Q,B,C四点为顶点的四边形是平行四边形时,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y= ![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,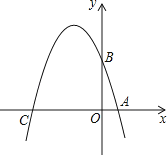
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com