
如图,已知△ABC是边长为6cm的等边三角形,动点P,Q同时从A、B两点出发,分别沿AB,BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),
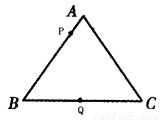
解答下列问题:
(1)当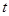 为何值时,△BPQ为直角三角形;
为何值时,△BPQ为直角三角形;
(2)设△BPQ的面积为S(cm2),求S与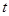 的函数关系式;
的函数关系式;
(3)作QR∥BA交AC于点R,连结PR,当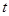 为何值时,△APR∽△PRQ ?
为何值时,△APR∽△PRQ ?
(1) 或3;(2)
或3;(2)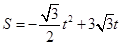 ;(3)
;(3) .
.
【解析】
试题分析:(1) 分两种情况考虑:(i)当PQ⊥BC时,如图所示,由速度是1厘米/秒,时间是t秒,利用速度×时间=路程表示出AP与BQ的长,再由AB-AP表示BP,由三角形ABC为等边三角形,得到∠B=60°,在直角三角形BPQ中,利用锐角三角函数定义及特殊角的三角函数值列出关于t的方程,求出方程的解即可得到t的值;(ii)当QP⊥AB时,如图所示,由速度是1厘米/秒,时间是t秒,利用速度×时间=路程表示出AP与BQ的长,再由AB-AP表示BP,由三角形ABC为等边三角形,得到∠B=60°,在直角三角形BPQ中,利用锐角三角函数定义及特殊角的三角函数值列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
(2)根据∠B为60°特殊角,过Q作QE⊥AB,垂足为E,则BQ、BP、高EQ的长可用t表示,S与t的函数关系式也可求;
(3)由题目线段的长度可证得△CRQ为等边三角形,进而得出四边形EPRQ是矩形,由△APR∽△PRQ,可得出∠QPR=60°,利用60°的特殊角列出一方程即可求得t的值.
试题解析:(1)分两种情况考虑:(i)当PQ⊥BC时,如图1所示:
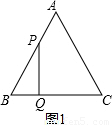
由题意可得:AP=tcm,BQ=2t厘米,BP=(6-t)厘米,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,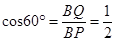
即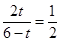 ,
,
解得:t= (秒);
(秒);
(ii)当QP⊥AB时,如图2所示:
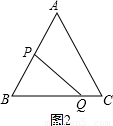
由题意可得:AP=tcm,BQ=2t厘米,BP=(6-2t)厘米,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,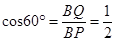 ,即
,即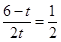 ,
,
解得:t=3(秒),
综上所述,t= 或3时,△BPQ为直角三解形;
或3时,△BPQ为直角三解形;
(2)如图3,过Q作QE⊥AB,垂足为E
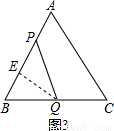
由QB=2t,得QE=2t•sin60°=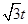
由AP=t,得PB=6-t
∴S△BPQ= ×BP×QE=
×BP×QE= (6-t)×
(6-t)×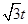 =
=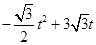
(3)如图4,∵QR∥BA,
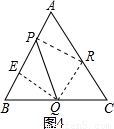
∴∠QRC=∠A=60°,∠RQC=∠B=60°
∴△QRC是等边三角形,
∴QR=RC=QC=6-2t,
∵BE=BQ•cos60°= ×2t=t,
×2t=t,
∴EP=AB-AP-BE=6-t-t=6-2t,
∴EP∥QR,EP=QR,
∴四边形EPRQ是平行四边形,
∴PR=EQ=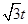
又∵∠PEQ=90°,
∴∠APR=∠PRQ=90°,
∵△APR∽△PRQ,
∴∠QPR=∠A=60°,
∴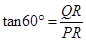 ,即
,即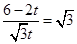 ,
,
解得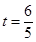 ,
,
∴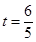 时,△APR∽△PRQ.
时,△APR∽△PRQ.
考点: 等边三角形的性质;一元一次方程的应用.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
 的坐标为(-1,0).
的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:
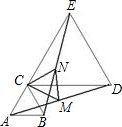 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com