
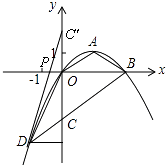
【题目】如图,顶点为A( ![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
【答案】
(1)
解:∵抛物线顶点为A( ![]() ,1),
,1),
设抛物线解析式为y=a(x﹣ ![]() )2+1,
)2+1,
将原点坐标(0,0)在抛物线上,
∴0=a( ![]() )2+1
)2+1
∴a=﹣ ![]() .
.
∴抛物线的表达式为:y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:令y=0,得 0=﹣ ![]() x2+
x2+ ![]() x,
x,
∴x=0(舍),或x=2 ![]()
∴B点坐标为:(2 ![]() ,0),
,0),
设直线OA的表达式为y=kx,
∵A( ![]() ,1)在直线OA上,
,1)在直线OA上,
∴ ![]() k=1,
k=1,
∴k= ![]() ,
,
∴直线OA对应的一次函数的表达式为y= ![]() x.
x.
∵BD∥AO,
设直线BD对应的一次函数的表达式为y= ![]() x+b,
x+b,
∵B(2 ![]() ,0)在直线BD上,
,0)在直线BD上,
∴0= ![]() ×2
×2 ![]() +b,
+b,
∴b=﹣2,
∴直线BD的表达式为y= ![]() x﹣2.
x﹣2.
由 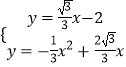
得交点D的坐标为(﹣ ![]() ,﹣3),
,﹣3),
令x=0得,y=﹣2,
∴C点的坐标为(0,﹣2),
由勾股定理,得:OA=2=OC,AB=2=CD,OB=2 ![]() =OD.
=OD.
在△OAB与△OCD中,
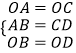 ,
,
∴△OAB≌△OCD.
(3)
解:点C关于x轴的对称点C'的坐标为(0,2),
∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,
∴PO∥DQ.
∴△C'PO∽△C'DQ.
∴ ![]() ,
,
∴ ![]() ,
,
∴PO= ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0)
,0)
【解析】(1)用待定系数法求出抛物线解析式,(2)先求出直线OA对应的一次函数的表达式为y= ![]() x.再求出直线BD的表达式为y=
x.再求出直线BD的表达式为y= ![]() x﹣2.最后求出交点坐标C,D即可;(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
x﹣2.最后求出交点坐标C,D即可;(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.


科目:初中数学 来源: 题型:
【题目】某校要将一块长为a米,宽为b米的长方形空地设计成花园,现有如下两种方案供选择.
方案一:如图1,在空地上横、竖各铺一条宽为4米的石子路,其余空地种植花草.
方案二:如图2,在长方形空地中留一个四分之一圆和一个半圆区域种植花草,其余空地铺筑成石子路.
(1) 分别表示这两种方案中石子路(图中阴影部分)的面积(若结果中含有π,则保留)
(2) 若a=30,b=20,该校希望多种植物美化校园,请通过计算选择其中一种方案(π取3.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品. 
(1)如果随机翻1张牌,那么抽中20元奖品的概率为 .
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数 ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.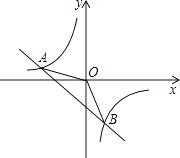
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级⑴班想买一些运动器材供班上同学阳光体育活动使用,班主任安排班长去商店买篮球和排球,下面是班长与售货员的对话:
班长:阿姨,您好! 售货员:同学,你好,想买点什么?

⑴根据这段对话,你能算出篮球和排球的单价各是多少吗?
⑵六一儿童节店里搞活动有两种套餐,1、套装打折:五个篮球和五个排球为一套装,套装打 八折:2、满减活动:999 减 100,1999 减 200;两种活动不重复参与,学校需要 15个篮球,13 个排球作为奖品,请问如何安排购买更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
我们知道:一条线段有两个端点,线段![]() 和线段
和线段![]() 表示同一条线段. 若在直线
表示同一条线段. 若在直线![]() 上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了
上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了![]() 个不同的点,共有线段条.(用含
个不同的点,共有线段条.(用含![]() 的代数式表示)
的代数式表示)
类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线,则所得图形中共有 个锐角;
(2)若引出![]() 条射线,则所得图形中共有 个锐角.(用含
条射线,则所得图形中共有 个锐角.(用含![]() 的代数式表示)
的代数式表示)
拓展应用:
一条铁路上共有8个火车站,若一列火车往返过程中必须停靠每个车站,则铁路局需为这条线路准备多少种车票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边AB在x轴上,点B与原点O重合,已知点A(﹣2,0),AC= ![]() ,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x﹣4上时,则平移的距离是( )
,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x﹣4上时,则平移的距离是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com