
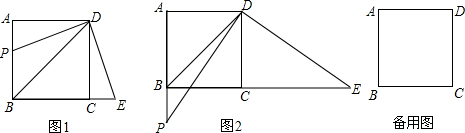
分析 (1)根据已知和图形证明△PAD≌△ECD,得到AP=CE,根据AB=$\frac{\sqrt{2}}{2}$BD,得到答案;
(2)与(1)的方法类似,求出结论;
(3)分P在线段AB上和P在AB延长线上两种情况进行讨论,根据三角形全等和勾股定理证明结论.
解答 证明:(1)∵四边形ABCD是正方形,
∴∠A=∠ADC=∠BCD=∠DCE=90°,AD=CD,
∵DE⊥PD,
∴∠ADC=∠PDE=90°,
∴∠ADP=90°-∠PDC=∠CDE,
∴△PAD≌△ECD,
∴AP=CE,
∴BP+CE=BP+AP=AB=$\frac{\sqrt{2}}{2}$BD;
(2)CE-BP=$\frac{\sqrt{2}}{2}$BD;
理由:△PAD≌△ECD,
∴CE=AP,
∴CE-BP=AP-BP=AB=$\frac{\sqrt{2}}{2}$BD;
(3)①当P在线段AB上时,
如图1所示,在BC上取一点G使得BG=BP,连接MG、NG,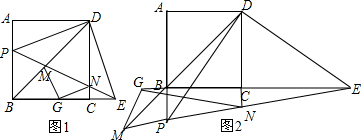
∵△APD≌△CED,
∵AP=CE,PD=ED,
∴△PED是等腰直角三角形,
∴AB=BC=AP+BP=BG+CG,
∴CG=CE,
∴可证△NCG≌△NCE,
∴NG=NE,∠NGC=∠NEC,
∵∠PBM=∠GBM=45°,BP=BG,BM=BM,
∴△BPM≌△BGM
∴PM=GM,∠MGB=∠MPB,
又∠NEC+∠MPB=90°,
∴∠NGC+∠MGB=90°,
∴∠MGN=90°,
∴MN=$\sqrt{M{G}^{2}+N{G}^{2}}$=5,
∴PE=PM+MN+EN=3+5+4=12,
∴PD=$\frac{\sqrt{2}}{2}$PE=6$\sqrt{2}$;
②当P在AB延长线上时,
如图2所示,延长CB至G,使得CG=CE,连接MG、NG,
∵AP=CE,
∴CE-BC=CG-BC=AP-AB=BP=BG,
同①可证△△BMG≌△BMP,△CNG≌△CNE,
∴PM=GM,GN=EN,∠BGM=∠BPM=90°+∠CEN=90°+CGN,
∴∠CGN=∠BGM-90°=∠BGM-∠MGN,
∴∠MGN=90°,
∴MN=$\sqrt{M{G}^{2}+N{G}^{2}}$=5,
∴PN=MN-PM=5-3=2,
∴PE=PN+EN=2+4=6,
∴PD=$\frac{\sqrt{2}}{2}$PE=3$\sqrt{2}$,
∴PD的长为3$\sqrt{2}$或6$\sqrt{2}$.
点评 本题考查的是四边形知识的综合运用,正确运用正方形的性质、正确作出辅助线构造全等三角形是解题的关键,注意分情况讨论思想的运用.


科目:初中数学 来源: 题型:解答题
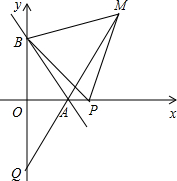 如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足(a-b)2+$\sqrt{{b}^{2}-16}$=0
如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足(a-b)2+$\sqrt{{b}^{2}-16}$=0查看答案和解析>>
科目:初中数学 来源: 题型:解答题
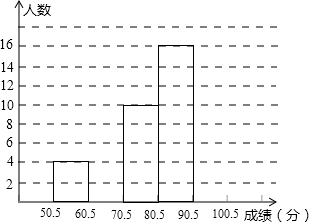 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.3-60.5 | 4 | 0.08 |
| 60.3-70.5 | 8 | 0.16 |
| 70.3-80.5 | 10 | 0.20 |
| 80.3-90.5 | 16 | 0.32 |
| 90.3-100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-3>y-3 | B. | 3-x>3-y | C. | x+2>y+3 | D. | $\frac{x}{3}>\frac{y}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com