
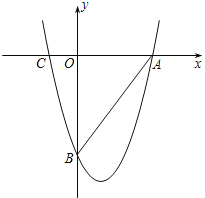
【题目】如图,抛物线![]() 与x轴交于A、C两点,与y轴交于B点.
与x轴交于A、C两点,与y轴交于B点.
(1)求△AOB的外接圆的面积;
(2)若动点P从点A出发,以每秒2个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动.问当t为何值时,以A、P、Q为顶点的三角形与△OAB相似?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBAN面积的最大值.
【答案】(1)![]() π;(2)当t=
π;(2)当t=![]() 时,以A、P、Q为顶点的三角形与△OAB相似;(3).①不存在;②M(
时,以A、P、Q为顶点的三角形与△OAB相似;(3).①不存在;②M(![]() ,-6),四边形CBAN面积的最大值为:
,-6),四边形CBAN面积的最大值为:![]() .
.
【解析】
试题(1)由题意得△AOB为直角三角形,分别求得抛物线y=![]() x2-
x2-![]() x-12与x轴、y轴的交点A、B的坐标,再根据勾股定理求得AB的长,最后根据直角三角形的性质即可求得结果;
x-12与x轴、y轴的交点A、B的坐标,再根据勾股定理求得AB的长,最后根据直角三角形的性质即可求得结果;
(2)由AP=2t,AQ=15-t,易求得AC=12,再分△APQ∽△AOB与△AQP∽△AOB两种情况根据相似三角形的性质即可求得结果;
(3)①先求得直线AB的函数关系式为y=![]() x-12,设点M的横坐标为x,则M(x,
x-12,设点M的横坐标为x,则M(x,![]() x-12),N(x,
x-12),N(x,![]() x2-
x2-![]() x-12),根据平行四边形的性质可得MN=OB=12,即可得到(
x-12),根据平行四边形的性质可得MN=OB=12,即可得到(![]() x-12)-(
x-12)-(![]() x2-
x2-![]() x-12)=12 ,而此方程的△<0,无实数根,故不存在这样的点M,使得四边形OMNB恰为平行四边形;
x-12)=12 ,而此方程的△<0,无实数根,故不存在这样的点M,使得四边形OMNB恰为平行四边形;
②由S四边形CBNA= S△ACB+ S△ABN="72+" S△ABN可得S△ABN=S△OBN+S△OAN-S△AOB=6x+(-2x2+12x+54)-54=-2x2+18x=-2(x-![]() )2+
)2+![]() ,根据二次函数的性质即可求得结果.
,根据二次函数的性质即可求得结果.
(1)由题意得:A(9,0),B(0,-12)
∴OA=9,OB=12,
∴AB=15
∴S=π·(![]() )2=
)2=![]() π;
π;
(2)AP=2t,AQ=15-t,易求AC=12,∴0≤t≤6
若△APQ∽△AOB,则![]() =
=![]() .∴t=
.∴t=![]() .
.
若△AQP∽△AOB,则![]() =
=![]() .∴t=
.∴t=![]() >6(舍去).
>6(舍去).
∴当t=![]() 时,以A、P、Q为顶点的三角形与△OAB相似.
时,以A、P、Q为顶点的三角形与△OAB相似.
(3)直线AB的函数关系式为y=![]() x-12.
x-12.
设点M的横坐标为x,则M(x,![]() x-12),N(x,
x-12),N(x,![]() x2-
x2-![]() x-12).
x-12).
若四边形OMNB为平行四边形,则MN=OB=12
∴(![]() x-12)-(
x-12)-(![]() x2-
x2-![]() x-12)=12
x-12)=12
即x2-9x+27=0
∵△<0,
∴此方程无实数根,
∴不存在这样的点M,使得四边形OMNB恰为平行四边形;
②∵S四边形CBNA= S△ACB+ S△ABN="72+" S△ABN
∵S△AOB=54,S△OBN=6x,S△OAN=![]() ·9·
·9·![]() =-2x2+12x+54
=-2x2+12x+54
∴S△ABN=S△OBN+S△OAN-S△AOB=6x+(-2x2+12x+54)-54=-2x2+18x=-2(x-![]() )2+
)2+![]()
∴当x=![]() 时,S△ABN最大值=
时,S△ABN最大值=![]()
此时M(![]() ,-6),S四边形CBNA最大=
,-6),S四边形CBNA最大=![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】山西是我国酿酒最早的地区之一,山西酿酒业迄今为止已有![]() 余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是
余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是![]() 元,经调查发现,当售价为
元,经调查发现,当售价为![]() 元时,每天可以售出
元时,每天可以售出![]() 瓶,售价每降低
瓶,售价每降低![]() 元,可多售出
元,可多售出![]() 瓶(售价不高于
瓶(售价不高于![]() 元)
元)
(1)售价为多少时可以使每天的利润最大?最大利润是多少?
(2)要使每天的利润不低于![]() 元,每瓶竹叶青酒的售价应该控制在什么范围内?
元,每瓶竹叶青酒的售价应该控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O1经过A(-4,2)、B(-3,3)、C(-1,-1)、O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.
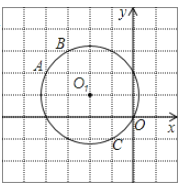
(1)在右边的平面直角坐标系中画出直线l,则直线l与⊙O1的交点坐标为 ;
(2)若⊙O1上存在点P,使得△APD为等腰三角形,则这样的点P有 个,试写出其中一个点P坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
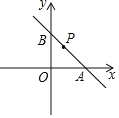
【题目】如图,在平面直角坐标系中,已知,A(2![]() ,0),B(0,2),C(
,0),B(0,2),C(![]() ,0),点P(m,n)为直线AB上一动点,若∠OPC=30°,则m的值为_____.
,0),点P(m,n)为直线AB上一动点,若∠OPC=30°,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
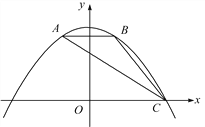
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地要建一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.如图建立平面直角坐标系,已知A(![]() ),顶点P(
),顶点P(![]() )
)
(1) 求抛物线的解析式
(2) 若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com