
【题目】如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°,∠EOD=67.5°的度数.
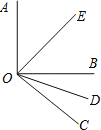
(1)求∠BOD的度数;
(2)∠AOE与∠BOC互余吗?请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )

A、9:4 B、3:2 C、![]() :
:![]() D、3
D、3![]() :2
:2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发,甲、乙两人到达N地后均停止骑行.已知M、N两地相距![]() km,设甲行驶的时间为x(h),甲、乙两人之间的距离为y(km),表示y与x函数关系的部分图象如图所示.请你解决以下问题:
km,设甲行驶的时间为x(h),甲、乙两人之间的距离为y(km),表示y与x函数关系的部分图象如图所示.请你解决以下问题:

(1)求线段BC所在直线的函数表达式;
(2)求点A的坐标,并说明点A的实际意义;
(3)根据题目信息补全函数图象.(须标明相关数据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,要测量一个沼泽水潭的宽度.现由于不能直接测量,小军是这样操作的:他在平地上选取一点C,该点可以直接到达A与B点,接着他量出AC和BC的距离,并找出AC与BC的中点E、F,连接EF,测量EF的长,于是他便知道了水潭AB的长等于2EF,小军的做法有道理吗?说明理由.你还有比小军更简单的方法吗?
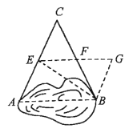
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
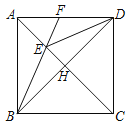
【题目】已知:如图,边长为1的正方形ABCD中,AC 、DB交于点H.DE平分∠ADB,交AC于点E.联结BE并延长,交边AD于点F.
(1)求证:DC=EC;
(2)求△EAF的面积.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图,如下:

(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学学生在学习等腰三角形性质“三线合一”时
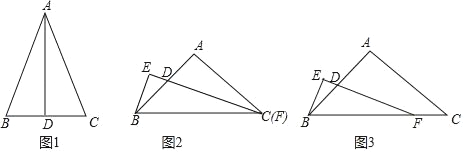
(1)(探究发现)如图1,在△ABC中,若AD平分∠BAC,AD⊥BC时,可以得出AB=AC,D为BC中点,请用所学知识证明此结论.
(2)(学以致用)如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且∠BFE=![]() ∠ACB,试探究线段BE和FD的数量关系,并证明.
∠ACB,试探究线段BE和FD的数量关系,并证明.
(3)(拓展应用)如图3,若顶点C与顶点F不重合,但是∠BFE=![]() ∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com