
С���Ҿ���ѧУ8ǧ�ף������糿С���ﳵ��ѧ;�У����г�ͻȻ����̥����ǡ��·���б������㣬�����Ӻ����ˣ����ӿ��ٶ��ﳵ��У�����Ǹ���С������ξ�������һ��ͼ��ͼ�����С����ʻ·��s������ʱ��t֮��ĺ�����ϵ�������ͼ��ش��������⣺
��1��С���ﳵ��ʻ�˶���ǧ��ʱ�����г�����̥�������˼����ӣ�
��2��С�����öʱ�䵽ѧУ�ģ�
��3��С����ǰ���ٶȺ�������ٶȷֱ��Ƕ��٣�
��4��������г�δ����̥����С��һֱ����ǰ�ٶ���ʻ����ô����ʵ������絽���������ٷ��ӣ�
��1��3ǧ�ף�5���ӣ�
��2 С����30���ӵ�ѧУ��
��3��С����ǰ���ٶȣ�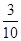 ǧ��/���ӣ�������ٶȣ�
ǧ��/���ӣ�������ٶȣ� ǧ��/���ӣ�
ǧ��/���ӣ�
��4���絽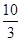 ���ӣ�
���ӣ�
���������������1��ͨ��ͼ���ϵĵ���������x��֮��Ĺ�ϵ��֪����ͼ��ͣ����5���ӣ�
��2��ͨ��ͼ���ϼ��ɿ���С����30���ӵ�ѧУ��
��3����Ӧ·�̳���ʱ�伴������ٶȣ�
��4���������ǰ�ٶ���Ҫ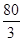 ���ӣ�����30��
���ӣ�����30��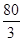 =
=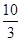 ������⣮
������⣮
�����������1��3ǧ�ף�5���ӣ�
��2��ͨ��ͼ���ϼ��ɿ���С����30���ӵ�ѧУ��
��3��С����ǰ���ٶȣ�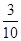 ǧ��/���ӣ�
ǧ��/���ӣ�
������ٶȣ� ǧ��/���ӣ�
ǧ��/���ӣ�
��4����ǰ�ٶ���Ҫ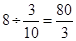 ���ӣ�30��
���ӣ�30��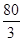 =
=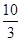 �����絽
�����絽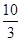 ���ӣ�
���ӣ�
���㣺һ�κ�����Ӧ�ã�


 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�� ��ӳ��ij��Ʒ������������������֮��Ĺ�ϵ��
��ӳ��ij��Ʒ������������������֮��Ĺ�ϵ�� ��ӳ�˸ò�Ʒ�����۳ɱ���������֮��Ĺ�ϵ������������������۳ɱ�ʱ�ò�Ʒ�ſ�ʼӯ������ͼ��֪���ò�Ʒ���������ﵽ____________ �������ò�Ʒ����ӯ����
��ӳ�˸ò�Ʒ�����۳ɱ���������֮��Ĺ�ϵ������������������۳ɱ�ʱ�ò�Ʒ�ſ�ʼӯ������ͼ��֪���ò�Ʒ���������ﵽ____________ �������ò�Ʒ����ӯ����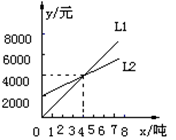
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ֱ�� ��˫����
��˫���� �ཻ��A��B���㣬��֪��A����2����1����
�ཻ��A��B���㣬��֪��A����2����1����
��1����k��ֵ����B�����ꣻ
��2������P��y���������ϵĶ��㣬�ж��м���λ����ʹ��PBOΪ���������Σ�ֱ��д����Ӧ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�жԻ�վ�����˴��ģ�ĸĽ����Ľ���Ļ�վ��ԭ�е���ͨ��Ʊ�����⣬�������Զ���ӡ��Ʊ��������Ʊ���ڣ���ͼ,�߶� ��
�� �ֱ��ʾij�մ�����8�㵽����11�㣬ÿ����ͨ��Ʊ�����۳��ij�Ʊ��
�ֱ��ʾij�մ�����8�㵽����11�㣬ÿ����ͨ��Ʊ�����۳��ij�Ʊ�� ���ţ���ÿ��������Ʊ�����۳��ij�Ʊ��
���ţ���ÿ��������Ʊ�����۳��ij�Ʊ�� ���ţ�������Ʊʱ��
���ţ�������Ʊʱ�� ��Сʱ���ĺ���ͼ��
��Сʱ���ĺ���ͼ��
��1���� ���ţ���
���ţ��� ��Сʱ���ĺ�������ʽ��
��Сʱ���ĺ�������ʽ��
��2�������쿪��������Ʊ���ڸ�������ͨ��Ʊ���ڸ�����2����������8�㵽����11�㣬���ִ��ڹ��۳��ij�Ʊ��Ϊ2400�ţ����쿪��������Ʊ���ڵĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����������ɳƺ�ӹ���һ��С������Ʒ������ȥij¥���˽������֪, �û�����Ʒ���ĵ�����8000Ԫ/ �������ͼ��ʾ����λ���ף�������Ŀ�δ�������Ϊ
�������ͼ��ʾ����λ���ף�������Ŀ�δ�������Ϊ �ף����۷���Ϊ�������ṩ�����������Żݷ�����
�ף����۷���Ϊ�������ṩ�����������Żݷ�����
����һ�������ĵ�����8000Ԫ/ �����г������������
���������������� �������
�������
��������������ԭ�����ܽ���9�۳��ۣ�
��1���� ��ʾ����һ�й���һ�û�����Ʒ�����ܽ���
��ʾ����һ�й���һ�û�����Ʒ�����ܽ��� ��ʾ�������й���һ�û�����Ʒ�����ܽ��ֱ����
��ʾ�������й���һ�û�����Ʒ�����ܽ��ֱ���� ��
�� ��
�� �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2���� ȡ��ֵʱ�������Żݷ������ܽ��һ���ࣿ
ȡ��ֵʱ�������Żݷ������ܽ��һ���ࣿ
��3�����������ֽ�����2012��1���ڽ��н���9��Ԫס�������������Ϊ6�꣬�ӿ�ʼ�������һ���������³�����������������0.5%��ÿ�»�������=ƽ��ÿ��Ӧ���Ĵ��������+����Ϣ������Ϣ=������ʣ���������������ʣ�
�������������һ����Ӧ���������Ƕ���Ԫ��
�ڼ�����������ʲ��䣬���������ڽ���� ��
�� ��
�� �������������µĻ�������ΪP����д��P��
�������������µĻ�������ΪP����д��P�� ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ı���ABCD��ƽ���ı��Σ���A��1��0����B��3��1����C��3��3��������������y= ��x��0���ĺ���ͼ����D����P��һ�κ���
��x��0���ĺ���ͼ����D����P��һ�κ���
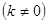 ��ͼ����÷���������ͼ���һ�������㣮
��ͼ����÷���������ͼ���һ�������㣮
��1�����������Ľ���ʽ��
��2��ͨ�����㣬˵��һ�κ���
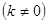 ��ͼ��һ������C��
��ͼ��һ������C��
��3������һ�κ���
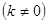 ����y��x�����������ʱ��ȷ����P�ĺ������ȡֵ��Χ������д�����̣���
����y��x�����������ʱ��ȷ����P�ĺ������ȡֵ��Χ������д�����̣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪ij�����ƻ��ÿ���302m3ľ��ΪijѧУ����500�����Σ�����У1250��ѧ��ʹ�ã��ó����������η�ΪA��B�����ͺţ��й��������£�
| �����ͺ� | һ����������ѧ����������λ���ˣ� | ����һ����������ľ�ģ���λ��m3�� | һ�����ε������ɱ�����λ��Ԫ�� | һ�����ε��˷ѣ���λ��Ԫ�� |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ˮ��ijУΪ�˿�չ����������������蹺��ijһƷ�Ƶ���ë�ס��������о���ÿֻ3Ԫ�ļ۸���ۣ�����һ���Թ�����һƷ����ë����100ֻ���û���ʵ���Żݣ��׳���ÿֻ��ë��ԭ�۵İ��۳��ۣ��ҳ�����15ֻ��ë���������ë��ÿֻ��ԭ�۵ľ��۳��ۣ�
��1��������ѡһ���У�һ���Թ���x��x��100��xΪ������ֻ��Ʒ����ë��д������Ǯy��Ԫ����x֮��ĺ�����ϵʽ��
��2����������260ֻ��Ʒ����ë�������ڼ׳����Լ׳��е��Żݷ�ʽ����һ���֣�ʣ�µ������ҳ������ҳ��е��Żݷ�ʽ������260ֻ��Ʒ����ë��������Ҫ������ԪǮ����ʱ�ڼס��������зֱ����Ʒ����ë�����ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�Ӽص��ҵأ�����һ��ƽ·��Ȼ����һ������·��С���ﳵ�Ӽس����������ҵغ�����ԭ·���ؼأ�;����Ϣ��һ��ʱ�䡣����С���ﳵ��ƽ·�����¡�����ʱ�ֱ𱣳�����ǰ��.��֪С���ﳵ���µ��ٶȱ�ƽ·�ϵ��ٶ�ÿСʱ��5km�����µ��ٶȱ���ƽ·�ϵ��ٶ�ÿСʱ��5km����С������xh�������y km�ĵط���ͼ�е�����OABCDE��ʾy��x֮��ĺ�����ϵ.
��1��С���ﳵ��ƽ·�ϵ��ٶ�Ϊ km/h����;����Ϣ�� h��
��2�����߶�AB��BC����ʾ��y�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3�����С�����ξ���;��ijһ�ص��ʱ����Ϊ0.15h����ô�õص���ض�Զ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com