

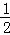 AB,然后求解即可;
AB,然后求解即可; BC,同理求出MG=
BC,同理求出MG= AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积即可;
AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积即可;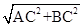 =
=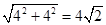 ,∵M是AB的中点,∴CM⊥AB,AM=CM=
,∵M是AB的中点,∴CM⊥AB,AM=CM=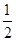 AB=
AB=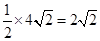 ,∴阴影部分的面积=
,∴阴影部分的面积=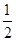 AM•CM=
AM•CM=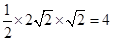 ;
;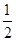 BC=
BC=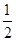 ×4=2,同理可得,MG=
×4=2,同理可得,MG=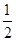 AC=
AC=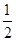 ×4=2,∴四边形DCGM是正方形,∴阴影部分的面积=22=4;
×4=2,∴四边形DCGM是正方形,∴阴影部分的面积=22=4;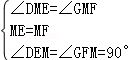 ,∴△DME≌△GMF(ASA),∴S△DME=S△GMF,∴阴影部分的面积=正方形ECMF的面积,∵M是AB的中点,∴ME是△ABC的中位线,∴ME=
,∴△DME≌△GMF(ASA),∴S△DME=S△GMF,∴阴影部分的面积=正方形ECMF的面积,∵M是AB的中点,∴ME是△ABC的中位线,∴ME=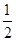 BC=
BC=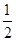 ×4=2,∴正方形ECMF的面积=22=4,∴阴影部分的面积=4.
×4=2,∴正方形ECMF的面积=22=4,∴阴影部分的面积=4.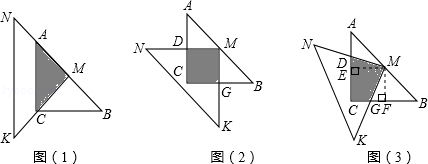


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com