
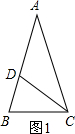
我们知道Rt△ABC中,∠A=![]() 时,就有BC2=AC2+AB2,反过来在△ABC中,若有AC2+AB2=BC2,是否存在∠A=
时,就有BC2=AC2+AB2,反过来在△ABC中,若有AC2+AB2=BC2,是否存在∠A=![]() 这样的结论呢?下面就这个问题我们进行探究.
这样的结论呢?下面就这个问题我们进行探究.

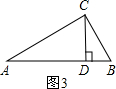
已知△ABC中,AC2+AB2=BC2.
求证:∠A=![]() .
.
证明:作![]() ,使
,使![]() =
=![]() ,
,
![]() =AB,
=AB,![]() =AC,
=AC,
∴![]() =
=![]() +
+![]() .
.
∴![]() =AB2+AC2.又∵BC2=AB2+AC2,
=AB2+AC2.又∵BC2=AB2+AC2,
∴_____________
在△ABC和![]() 中,
中,

∴_____________
∴_____________
(1)补充上述证明过程空缺的部分;
(2)上面已证的命题就是勾股定理的逆定理,可以直接运用上述的结论解决下面的问题:
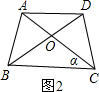
已知正方形ABCD,AB=a,点E为AB的中点,点F在AD边上,且AF=![]() AD,用两种不同的方法证明:EF⊥CE.
AD,用两种不同的方法证明:EF⊥CE.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
| CB |
| AC |
| AC |
| AB |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AC |
| BC |
| 3 |
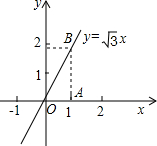 数y=ax+a-
数y=ax+a-| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |


| 5 |
| 5 |

| 10 |

| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: ,试求sad A的值
,试求sad A的值
|
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com