练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在平面直角坐标系中，平行四边形ABCD的顶点A、D的坐标分别是(0，0)，(2，3)，AB=5，则顶点C的坐标是（ ）

    A. (3，7)B. (5，3)C. (7，3)D. (8，2)

    【答案】C

    【解析】

    分别过点D，点C作垂线垂直于x轴于E，F，如解析中的图所示，证明三角形ADE与三角形BCF全等，得到BF的值，则点C的横坐标的值即为AB+BF=AF的长度.又因为DC∥AB，所以点C的纵坐标与D的纵坐标相等.

    如图所示：过点D，C分别作x轴的垂线于点E，F

    ∵四边形ABCD是平行四边形

    ∴AD=BC，

    ∵

    ∴

    在与中

    ∴

    ∴AE=BF

    ∵AE是点D横坐标的值，AE=2

    ∴AF=AB+BF=7

    ∴点C的横坐标的值为7

    又∵ DC∥AB

    ∴点C的纵坐标的值等于点D纵坐标的值，即为3

    ∴点C的坐标为（7，3）

    故答案为C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图,已知直线a∥b,点A在直线a上,点B. C在直线b上,点P在线段AB上,∠1=70,∠2=100，求∠PCB的度数.

    （2）下表是某商行一种商品的销售情况，该商品原价为560元，随着不同幅度的降价（单位：元），日销量（单位：件）发生相应变化如下表：

    降价（元）

    5

    10

    15

    20

    25

    30

    35

    日销量（件）

    78

    81

    84

    87

    90

    93

    96

    ①根据表格所列出的变化关系，请你估计降价之前的日销量是多少件？

    ②根据表格所列出的变化关系，请直接写出与的关系式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，，点是射线上一动点（与点不重合），、分别平分和，分别交射线于点、.

    （1）求的度数；

    （2）当点运动时，与之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律.

    （3）当点运动到使时，求的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，正比例函数y＝ax的图象与反比例函数y＝的图象交于点A（3，2）

    （1）试确定上述正比例函数和反比例函数的表达式；

    （2）根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？

    （3）点M（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两城市之间开通了动车组高速列车。已知每隔2h有一列速度相同的动车组列车从甲城开往乙城。如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象。请根据图中的信息，解答下列问题：

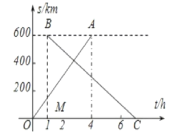
    (1)从图象看,普通快车发车时间比第一列动车组列车发车时间___1h(填“早”或“晚”)，点B的纵坐标600的实际意义是___；

    (2)请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象；

    (3)若普通快车的速度为100km/h，

    ①求BC的表达式，并写出自变量的取值范围；

    ②第二列动车组列车出发多长时间后与普通快车相遇?

    ③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】微商小明投资销售一种进价为每条元的围巾．销售过程中发现，每月销售量（件）与销售单价（元）之间的关系可近似的看作一次函数： ，销售过程中销售单价不低于成本价，而每条的利润不高于成本价的．

    （）设小明每月获得利润为（元），求每月获得利润（元）与销售单价（元）之间的函数关系式，并确定自变量的取值范围．

    （）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？

    （）如果小明想要每月获得的利润不低于元，那么小明每月的成本最少需要多少元？（成本进价销售量）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．

    探究一：求不等式|x﹣1|＜2的解集

    （1）探究|x﹣1|的几何意义

    如图①，在以O为原点的数轴上，设点A′对应的数是x﹣1，有绝对值的定义可知，点A′与点O的距离为

    |x﹣1|，可记为A′O=|x﹣1|．将线段A′O向右平移1个单位得到线段AB，此时点A对应的数是x，点B对应的数是1．因为AB=A′O，所以AB=|x﹣1|，因此，|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB．

    （2）求方程|x﹣1|=2的解

    因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2，所以方程的解为3，﹣1．

    （3）求不等式|x﹣1|＜2的解集

    因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围．请写出这个解集：_________________________________．

    探究二：探究的几何意义

    （1）探究的几何意义

    如图③，在直角坐标系中，设点M的坐标为（x，y），过M作MP⊥x轴于P，作MQ⊥y轴于Q，则P点坐标为（x，0），Q点坐标为（0，y），OP=|x|，OQ=|y|，在Rt△OPM中，PM=OQ=|y|，则，因此，的几何意义可以理解为点M（x，y）与点O（0，0）之间的距离MO．

    （2）探究的几何意义

    如图④，在直角坐标系中，设点A′的坐标为（x﹣1，y﹣5），由探究二（1）可知，，将线段A′O先向右平移1个单位，再向上平移5个单位，得到线段AB，此时点A的坐标为（x，y），点B的坐标为（1，5），因为AB=A′O，所以，因此的几何意义可以理解为点A（x，y）与点B（1，5）之间的距离AB．

    （3）探究的几何意义，根据探究二（2）所得的结论，请写出的几何意义可以理解为：________________．

    （4）的几何意义可以理解为：________________________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一家蔬菜公司收购到某种绿色蔬菜200吨，准备加工后进行销售，销售后获利的情况如下表所示：

    销售方式

    粗加工后销售

    精加工后销售

    每吨获利（元）

    500

    800

    已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行．受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完．

    （1）如果要求20天刚好加工完200吨蔬菜，则公司应安排几天精加工，几天粗加工？

    （2）如果先进行精加工，然后进行粗加工．

    ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；

    ②若要求在不超过16天的时间内，将200吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形ABCD绕点A按逆时针方向旋转，得到矩形AEFG，E点正好落在边CD上，连接BE，BG，且BG交AE于P．

    （1）求证：∠CBE=∠BAE；

    （2）求证：PG=PB；

    （3）若AB=，BC=3，求出BG的长．

    查看答案和解析>>

    同步练习册答案