
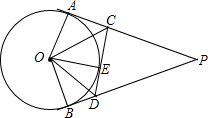
 如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )
如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D,下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据切线长定理,可判断①②正确;利用四边形的内角和=360°,可判断③正确;将△PCD的周长转化为PA+PB,可判断④正确.
解答 解:∵PA、PB是⊙O的切线,
∴PA=PB,∠ACO=∠DCO,故①②正确;
∵PA、PB、CD是⊙O的切线,
∴CA=CE,DE=DB,∠OBD=∠OED=90°,
∴∠BOE+∠BDE=360°-∠OBD-∠OED=180°,
∴∠BOE和∠BDE互补,故③正确;
∴△PCD的周长=PC+CE+DE+PD=PC+CA+PD+DB=PA+PB=2PA,故④正确.
故选D.
点评 本题考查了切线的性质及切线长定理,解答本题的关键是熟练掌握:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.


科目:初中数学 来源: 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
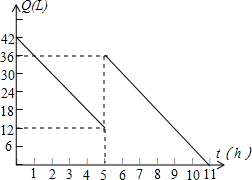 机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
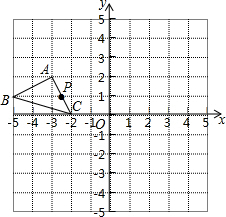 如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位.平面直角坐标系和△ABC的位置如图所示.
如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位.平面直角坐标系和△ABC的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
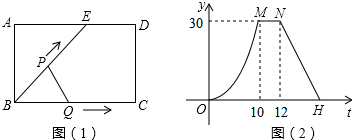
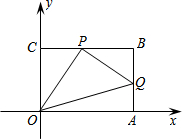 已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(6,0)、C(0,4),点P在BC边上运动,过P作PQ⊥OP,交AB边于Q,则AQ的最小值为$\frac{7}{4}$.
已知:如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(6,0)、C(0,4),点P在BC边上运动,过P作PQ⊥OP,交AB边于Q,则AQ的最小值为$\frac{7}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:
如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a2=a6 | B. | $\sqrt{9}$=±3 | C. | ($\frac{1}{2}$)-1=-2 | D. | (π-3.14)0=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com