
����Ŀ��ij��ѧ������������д��������ÿλѧ����д����![]() �������������������鲿��ѧ������д����������Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ���֣�������Ϣ����������⣺
�������������������鲿��ѧ������д����������Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ���֣�������Ϣ����������⣺
��� | ��ȷ���� | ���� |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|


��1����ͳ�Ʊ��У�![]() ��
��![]() ��
��
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ����D��������Ӧ��Բ�ĽǵĶ���Ϊ ��
��4������У����![]() ��ѧ���������д��ȷ����������
��ѧ���������д��ȷ����������![]() ����Ϊ���ϸ��������������ѧ��α�����д���ϸ��ѧ������.
����Ϊ���ϸ��������������ѧ��α�����д���ϸ��ѧ������.
���𰸡���1��![]() ,
,![]() ����2����ͼ����������3��
����2����ͼ����������3��![]() ����4��375
����4��375
��������
��1����������ͼ������ͼȷ��A�������������ռ�İٷֱȣ�������������������õ������������ȥͳ��ͼ����֪���������ɵ�a��ֵ��
�۲�����ͼ��֪B�������Ϊ20�ˣ���B����������Ե�������������ٳ���100%���������b��ֵ��
���ڣ�2���ɣ�1��������a��ֵ���ɽ�����ͳ��ͼ����������
���ڣ�3����360����ԡ�D�顱��ռ�İٷֱȣ��õ�����Ӧ��Բ�ĽǵĶ�����
���ڣ�4����д��ȷ����������16������A���B�飬�ɴ�������ϸ�������ռ�İٷֱȣ������ó���У������д�������ϸ��ѧ������.
��1��������������10��10%=100���ˣ���
��a=100-10-15-25-20=30���ˣ���
b= ![]() ��100%=20%.
��100%=20%.
��2��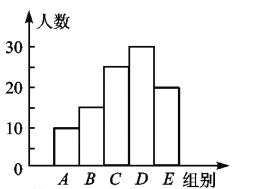
��3������ͳ��ͼ�С�D�顱����Ӧ��Բ�ĽǵĶ�����360���30%=108��.
��4������������ѧ���α�����д���ϸ��ѧ������Լ��1500��(10%+15%)=375���ˣ�.
������������ѧ���α�����д���ϸ��ѧ������Լ��375��.


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵĸߣ�����ABD��AD�۵��õ���AED����E����CD�ϣ���B=50������C=30����
��1����գ���BAD= �ȣ�
��2�����CAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾���A����2��0����B����3��3����ԭ��O������ΪC��

��1���������ߵĺ�������ʽ��
��2�����D���������ϣ���E�������ߵĶԳ����ϣ����ı���AODE��ƽ���ı��Σ����D�����꣮
��3������BC��x���ڵ�F��y�����Ƿ���ڵ�P��ʹ����POC����BOF���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ����4���������ν�����̬�����Ρ����磺ij���������߳��ֱ���5��6��8����Ϊ![]() ����������������dz�̬�����Ρ�
����������������dz�̬�����Ρ�
��1������ABC���߳��ֱ���2��![]() ��4�����������_________��̬�����Σ�����������������������
��4�����������_________��̬�����Σ�����������������������
��2����Rt��ABC�dz�̬�����Σ���������ε����߳�֮��Ϊ__________________���밴��С�������У���
��3����ͼ��Rt��ABC�У���ACB=90�㣬BC=6����DΪAB���е㣬����CD������BCD�dz�̬�����Σ����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺![]() ��2�����㣺
��2�����㣺![]()
��3���ⷽ�̣�![]()
��4���ⲻ��ʽ�� ���������ǵĽ⼯�������ϱ�ʾ����.
���������ǵĽ⼯�������ϱ�ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�����EFGH��ֱ��l��ͬ�࣬��AD��EH��ֱ��l�ϣ���AD=5cm��EH=4cm��EF=3cm������������ABCD������������EFGH��ֱ��l�����ƶ�������BF��CG����BF+CG����СֵΪ_____________cm

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
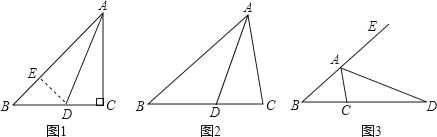
����Ŀ������ABC�У���ACB=2��B����ͼ��������C=90�㣬ADΪ��BAC�Ľ�ƽ����ʱ����AB�Ͻ�ȡAE=AC������DE����֤AB=AC+CD��
��1����ͼ��������C��90�㣬ADΪ��BAC�Ľ�ƽ����ʱ���߶�AB��AC��CD����������������ϵ������Ҫ֤������ֱ��д����IJ��룺
��2����ͼ������ADΪ��ABC�����ƽ����ʱ���߶�AB��AC��CD����������������ϵ����д����IJ��룬������IJ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�BEƽ�֡�ABC�ҽ���AD�ڵ�E�����AB=6cm��BC=10cm��
������ABCD���ܳ������߶�DE�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
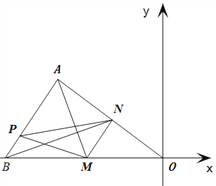
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���AOB���������������ֱ���A(-4,3)��B(-6,0)�� O��ԭ�㣮��M��OB��������O��B��һ���㣬����M��MN//AB����P��AB���ϵ�����㣬����AM��PM��PN��BN�����![]() .
.
��1�����OA����ֱ�ߵĽ���ʽ���������M������Ϊ(-1,0)ʱ����N�����꣮
��2���� ![]() =
=![]() ʱ�����ʱ��N�����꣮
ʱ�����ʱ��N�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com