
分析 (1)设甲种君子兰每株成本为x元,乙种君子兰每株成本为y元.此问中的等量关系:①购进甲种2株,乙种3株,则共需要成本1700元;②购进甲种3株,乙种1株,则共需要成本1500元;依此列出方程求解即可;
(2)结合(1)中求得的结果,根据题目中的不等关系:成本不超过30000元;列不等式进行分析.
解答 解:(1)设甲种君子兰每株成本为x元,乙种君子兰每株成本为y元,依题意有
$\left\{\begin{array}{l}{2x+3y=1700}\\{3x+y=1500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=400}\\{y=300}\end{array}\right.$.
故甲种君子兰每株成本为400元,乙种君子兰每株成本为300元.
(2)设购进甲种君子兰a株,则购进乙种君子兰(3a+10)株,依题意有
400a+300(3a+10)≤30000,
解得a≤$\frac{270}{13}$.
∵a为整数,
∴a最大为20.
故最多购进甲种君子兰20株.
点评 考查了二元一次方程组的应用,一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
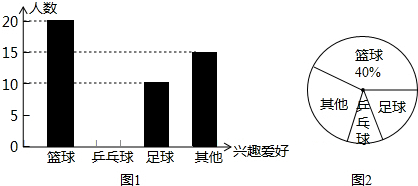
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2=2 | B. | x2-(k+1)x+(k+1)=0 | C. | 2x2-$\sqrt{2}$x+1=0 | D. | 1+$\frac{x}{x-1}$=$\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )| A. | 2海里 | B. | 2sin55°海里 | C. | 2cos55°海里 | D. | 2tan55°海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
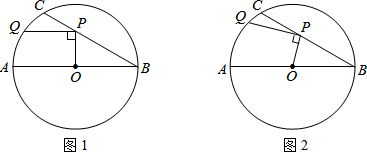
 ⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
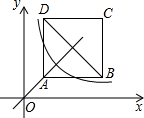 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com