
已知抛物线y=x2﹣2x+c与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
(1)求D点的坐标;
(2)如图1,连接AC,BD并延长交于点E,求∠E的度数;
(3)如图2,已知点P(﹣4,0),点Q在x轴下方的抛物线上,直线PQ交线段AC于点M,当∠PMA=∠E时,求点Q的坐标.

考点:
二次函数综合题.
分析:
(1)将点A的坐标代入到抛物线的解析式求得c值,然后配方后即可确定顶点D的坐标;
(2)连接CD、CB,过点D作DF⊥y轴于点F,首先求得点C的坐标,然后证得△DCB∽△AOC得到∠CBD=∠OCA,根据∠ACB=∠CBD+∠E=∠OCA+∠OCB,得到∠E=∠OCB=45°;
(3)设直线PQ交y轴于N点,交BD于H点,作DG⊥x轴于G点,增大△DGB∽△PON后利用相似三角形的性质求得ON的长,从而求得点N的坐标,进而求得直线PQ的解析式,
设Q(m,n),根据点Q在y=x2﹣2x﹣3上,得到﹣![]() m﹣2=m2﹣2m﹣3,求得m、n的值后即可求得点Q的坐标.
m﹣2=m2﹣2m﹣3,求得m、n的值后即可求得点Q的坐标.
解答:
解:(1)把x=﹣1,y=0代入y=x2﹣2x+c得:1+2+c=0
∴c=﹣3
∴y=x2﹣2x﹣3=y=(x﹣1)2﹣4
∴顶点坐标为(1,﹣4);
(2)如图1,连接CD、CB,过点D作DF⊥y轴于点F,
由x2﹣2x﹣3=0得x=﹣1或x=3
∴B(3,0)
当x=0时,y=x2﹣2x﹣3=﹣3
∴C(0,﹣3)
∴OB=OC=3
∵∠BOC=90°,
∴∠OCB=45°,
BC=3![]()
又∵DF=CF=1,∠CFD=90°,
∴∠FCD=45°,CD=![]() ,
,
∴∠BCD=180°﹣∠OCB﹣∠FCD=90°.
∴∠BCD=∠COA
又∵![]()
∴△DCB∽△AOC,
∴∠CBD=∠OCA
又∵∠ACB=∠CBD+∠E=∠OCA+∠OCB
∴∠E=∠OCB=45°,
(3)如图2,设直线PQ交y轴于N点,交BD于H点,作DG⊥x轴于G点
∵∠PMA=45°,
∴∠EMH=45°,
∴∠MHE=90°,
∴∠PHB=90°,
∴∠DBG+∠OPN=90°
又∴∠ONP+∠OPN=90°,
∴∠DBG=∠ONP
又∵∠DGB=∠PON=90°,
∴△DGB=∠PON=90°,
∴△DGB∽△PON
∴![]()
即:![]() =
=![]()
∴ON=2,
∴N(0,﹣2)
设直线PQ的解析式为y=kx+b
则![]()
解得:
∴y=﹣![]() x﹣2
x﹣2
设Q(m,n)且n<0,
∴n=﹣![]() m﹣2
m﹣2
又∵Q(m,n)在y=x2﹣2x﹣3上,
∴n=m2﹣2m﹣3
∴﹣![]() m﹣2=m2﹣2m﹣3
m﹣2=m2﹣2m﹣3
解得:m=2或m=﹣![]()
∴n=﹣3或n=﹣![]()
∴点Q的坐标为(2,﹣3)或(﹣![]() ,﹣
,﹣![]() ).
).

点评:
本题考查了二次函数的综合知识,难度较大,题目中渗透了许多的知识点,特别是二次函数与相似三角形的结合,更是一个难点,同时也是中考中的常考题型之一.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
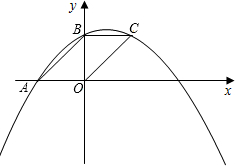 (1)求b+c的值;
(1)求b+c的值;查看答案和解析>>
科目:初中数学 来源: 题型:
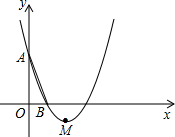 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com