


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
已知△ABC的一条边BC的长为5,另两边AB、AC的长是关于x的一元二次方程![]() 的两个实数根.
的两个实数根.
1.求证:无论![]() 为何值时,方程总有两个不相等的实数根;
为何值时,方程总有两个不相等的实数根;
2.当![]() 为何值时,△ABC是以BC为斜边的直角三角形;
为何值时,△ABC是以BC为斜边的直角三角形;
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省海安县曲塘中学附属初级中学九年级上学期期中考试数学卷 题型:解答题
(本题10分)已知△ABC的一条边BC的长为5,另两边AB、AC的长是关于x的一元二次方程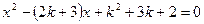 的两个实数根.
的两个实数根.
(1)求证:无论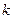 为何值时,方程总有两个不相等的实数根;
为何值时,方程总有两个不相等的实数根;
(2)当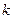 为何值时,△ABC是以BC为斜边的直角三角形;
为何值时,△ABC是以BC为斜边的直角三角形;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com