
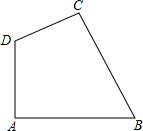
 如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.
如图,四边形ABCD中,∠A=90°,AB=5$\sqrt{3}$,BC=8,CD=6,AD=5.分析 (1)连接BD,在△ABD中,利用勾股定理求得BD的长;
(2)然后利用勾股定理的逆定理证明△BCD是直角三角形即可证得.
解答 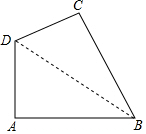 解:(1)连接BD,
解:(1)连接BD,
∵∠A=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10;
(2)A、B、C、D在同一个圆上.
证明:在直角△ABD中,BD=10,
在△BCD中,∵82+62=100,即BC2+CD2=BD2,
∴△BCD是直角三角形.
∴B、C、D在以BD为直径的圆上.
又∵△ABD是直角三角形,则A、B、D在以BD为直径的圆上.
∴点A、B、C、D在以BD为直径的圆上.
点评 本题考查了直角三角形的性质,直角三角形的三个顶点在以斜边为直径的圆上.


科目:初中数学 来源: 题型:解答题
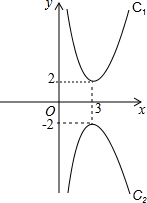 如图,在同一平面直角坐标系中,画出抛物线C1:y=(x-3)2+2和它关于x轴对称的抛物线C2,我们容易发现,抛物线C2的开口向下,形状与抛物线C1相同,其解析式是y=-(x-3)2-2,请运用轴对称的知识,求出抛物线C1关于y轴对称的抛物线C3的解析式.
如图,在同一平面直角坐标系中,画出抛物线C1:y=(x-3)2+2和它关于x轴对称的抛物线C2,我们容易发现,抛物线C2的开口向下,形状与抛物线C1相同,其解析式是y=-(x-3)2-2,请运用轴对称的知识,求出抛物线C1关于y轴对称的抛物线C3的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )| A. | 10$\sqrt{3}$米 | B. | 15米 | C. | 20$\sqrt{3}$米 | D. | 30米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com