
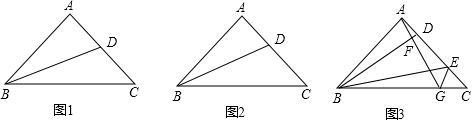
分析 (1)根据三角形的中线将三角形分成面积相等的两个三角形得:S△BCD=S△ABD,因此计算△ABD的面积就是△BCD的面积,代入面积公式计算即可;
(2)如图2,作辅助线,构建全等三角形,证明△ABD≌△EBD,则AB=EB,AD=DE,再证明△DEC是等腰直角三角形,根据BC=BE+CE可得结论;
(3)如图3,作辅助线构建全等三角形和直角三角形,证明△ABD≌△CAH,得AD=CH,∠ADB=∠H;得出CE=CH,所以继续证明△ECG≌△HCG,得∠CEG=∠H,从而得出结论.
解答 解:(1)如图1,在Rt△ABC中,AB=AC=8,
∵D是AC的中点,
∴AD=CD=$\frac{1}{2}$AC=4,
∴S△BCD=S△ABD=$\frac{1}{2}$AD•AB=$\frac{1}{2}$×8×4=16;
(2)数量关系为:BC=AB+AD.理由如下: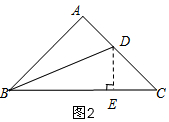
如图2,过D作DE⊥BC于E,
又∵∠BAC=90°,
∴∠BED=∠BAC=90°,
∵BD是∠ABC的角平分线,
∴∠ABD=∠EBD,
又∵BD=BD,
∴△ABD≌△EBD,
∴AB=EB,AD=DE,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠C=45°,
又∵∠CED=90°,
∴∠CDE=180°-∠CED-∠C=45°=∠C,
∴CE=DE,
又∵AB=EB,AD=DE,
∴BC=BE+CE=AB+DE=AB+AD;
(3)如图3,过点C作CH⊥AC,交AG的延长线于点H,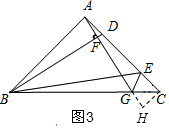
又∵∠BAC=90°,
∴∠HCA=∠DAB=90°,
∵∠BAC=90°,AF⊥BD,
∴∠DAF+∠ADF=90°,∠ABD+∠ADF=90°,
∴∠ABD=∠DAF,
又∵AB=AC,∠HCA=∠DAB,
∴△ABD≌△CAH,
∴AD=CH,∠ADB=∠H.
又∵AD=CE,
∴CH=CE.
∵∠ACB=45°,∠ACH=90°,
∴∠BCH=∠ACB=45°,
又∵GC=GC,CH=CE,
∴△ECG≌△HCG,
∴∠CEG=∠H,
又∵∠ADB=∠H,
∴∠ADB=∠CEG.
点评 本题是三角形的综合题,难度适中,考查了等腰直角三角形的性质和判定、全等三角形的性质和判定、三角形中线的性质,(2)和(3)问题的关键是作垂线,构建全等三角形,从而使问题得以解决.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
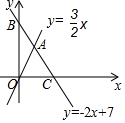 如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.
如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
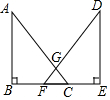 如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.
如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原质量 | 27 | 24 | 23 | 28 | 21 | 26 | 22 | 27 |
| 与基准数的差距 | 1 | -2 | -3 | 2 | -5 | 0 | -4 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com