
【题目】在A地到B地的快速通道某隧道建设,将由甲,乙两个工程队共同施工完成,据调查得知:甲,乙两队单独完成这项上程所需天数之比为4:5,若先由甲,乙两队合作40天,剩下的工程再乙队做10天完成,
(1)求甲.乙两队单独完成这取工程各需多少天?
(2)若此项工程由甲队做m天,乙队n天完成,
①请用含m的式子表示n;
②已知甲队每天的施工费为15万元,乙队每天的施工费用为10万元,若工程预算的总费用不超过1150万元,甲队工作的天数与乙队工作的天数之和不超过90天.请问甲、乙两队各工作多少天,完成此项工程总费用最少?最少费用是多少?
【答案】(1)甲,乙两队单独完成这取工程各需80,100天;(2)①n=100-![]() ②甲、乙两队各工作40,50天,完成此项工程总费用最少,最少费用是1100万元
②甲、乙两队各工作40,50天,完成此项工程总费用最少,最少费用是1100万元
【解析】
(1) 设甲,乙两队单独完成这取工程各需4x,5x天,甲每天完成 ![]() ,乙每天完成
,乙每天完成![]() ,然后列出方程(
,然后列出方程(![]() )×40+
)×40+![]() =1,解出即可,要检验;
=1,解出即可,要检验;
(2)根据(1)中所求即可列出①的方程
②令施工总费用为W万元,则可列出w=15m+10×(100-![]() )=
)=![]() m+1000,再根据两队施工的天数之和不超过90天,工程预算的总费用不超过1150万元,即可解答
m+1000,再根据两队施工的天数之和不超过90天,工程预算的总费用不超过1150万元,即可解答
(1)设甲,乙两队单独完成这取工程各需4x,5x天,
由题意得:(![]() )×40+
)×40+![]() =1
=1
解得:x=20,
经检验:x=20是原方程的根,
4x=80,5x=100,
答:甲,乙两队单独完成这取工程各需80,100天;
(2)①由题意得:n=(![]() )
)![]()
![]() =100-
=100-![]()
②令施工总费用为W万元,
则w=15m+10×(100-![]() )=
)=![]() m+1000
m+1000
∵两队施工的天数之和不超过90天,工程预算的总费用不超过1150万元,
∴![]() m+1000≤1150,m+(100-
m+1000≤1150,m+(100-![]() )≤90
)≤90
∴40≤m≤60,
∴当m=40时,完成此项工程总费用最少,
∴n=100-![]() ≤50,W=1100万元,
≤50,W=1100万元,
答:甲、乙两队各工作40,50天,完成此项工程总费用最少,最少费用是1100万元


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】为了迎接2018年高中招生考试,某中学对全校九年级进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下两幅不完整的统计图1和图2,请你根据图中所给的信息解答下列问题。
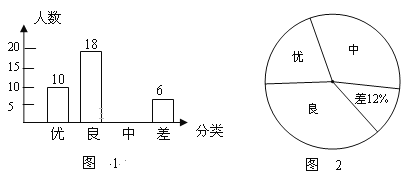
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中表示成绩为“优”的扇形所对的圆心角为 度;
(3)学校九年级共有600人参加这次数学考试,估计该校有多少名学生成绩可以达到优.
查看答案和解析>>
科目:初中数学 来源: 题型:
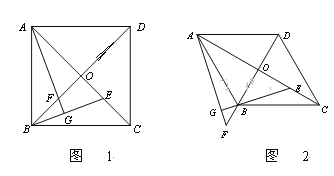
【题目】在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.
(1)如图1,若四边形ABCD是正方形,
①求证:△AOF≌△BOE;
②连接EF,判断EF与BC的位置关系,并说明理由。
(2)如图2,若四边形ABCD是菱形, ∠ABC=1200,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
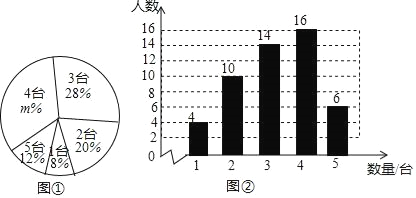
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
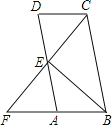
【题目】如图,已知平行四边形ABCD中,E为AD中点,CE延长线交BA延长线于点F.
(1)求证:CD=AF;
(2)若BC=2CD,求证:∠F=∠BCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
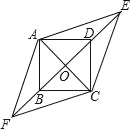
A. DE=1 B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com