练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，∠ABC=90°，D、E分别在BC、AC上，AD⊥DE，且AD=DE，点F是AE的中点，FD与AB相交于点M．

    （1）求证：∠FMC=∠FCM；

    （2）AD与MC垂直吗？并说明理由．


    （1）证明：∵△ADE是等腰直角三角形，F是AE中点，

    ∴DF⊥AE，DF=AF=EF，又∵∠ABC=90°，∠DCF，∠AMF都与∠MAC互余，

    ∴∠DCF=∠AMF，

    在△DFC和△AFM中，，∴△DFC≌△AFM（AAS），

    ∴CF=MF，∴∠FMC=∠FCM；

    （2）AD⊥MC，

    理由：由（1）知，∠MFC=90°，FD=EF，FM=FC，∴∠FDE=∠FMC=45°，

    ∴DE∥CM，∴AD⊥MC．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    写出一个三视图中主视图与俯视图完全相同的几何体的名称

    查看答案和解析>>

    科目：初中数学 来源： 题型：


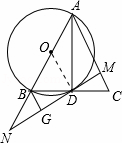
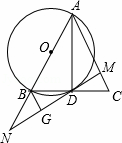
    如图，已知在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过D作MN⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于G．

    （1）求证：△BGD∽△DMA；

    （2）求证：直线MN是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若不等式组有解，则实数a的取值范围是（　　）

    　  A．a＜﹣36      B． a≤﹣36         C． a＞﹣36         D． a≥﹣36

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    七（一）班同学为了解某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据整理如下表（部分）：

    月均用水量x/m3

    0＜x≤5

    5＜x≤10

    10＜x≤15

    15＜x≤20

    x＞20

    频数/户

    12

    20

    3

    频率

    0.12

    0.07

    若该小区有800户家庭，据此估计该小区月均用水量不超过10m3的家庭约有　　户．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，点P（-2，3）关于原点对称的点Q的坐标为

    A．（2，-3） B．（2，3）  C．（3，-2） D．（-2，-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算=                 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某数学兴趣小组对线段上的动点问题进行探究，已知AB=8.

    问题思考：

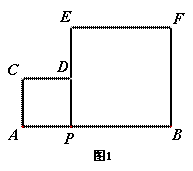
    如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.

    （1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值.

    （2）分别连接AD、DF、AF，AF交DP于点A，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由.

    问题拓展：

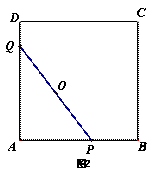
    （3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8.若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长。

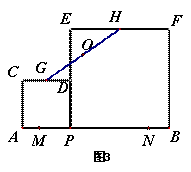
     (4)如图（3），在“问题思考”中，若点M、N是线段AB上的两点，且AM=BM=1，点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值.

        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一列数a1，a2，a3，…an，其中a1=﹣1，a2=，a3=，…，an=，则a1+a2+a3+…+a2014=　　．

    查看答案和解析>>

    同步练习册答案