
分析 (1)先化简括号内的式子,再根据有理数的除法可以化简题目中的式子,然后将a=4代入化简后的式子即可解答本题;
(2)先化简题目中的式子,然后根据a2+2a-15=0,可以解答本题.
解答 解:(1)$\frac{a-2}{{{a^2}-1}}$÷(a-1-$\frac{2a-1}{a+1}}$)
=$\frac{a-2}{(a+1)(a-1)}÷\frac{(a-1)(a+1)-(2a-1)}{a+1}$
=$\frac{a-2}{(a+1)(a-1)}×\frac{a+1}{{a}^{2}-1-2a+1}$
=$\frac{a-2}{(a+1)(a-1)}×\frac{a+1}{a(a-2)}$
=$\frac{1}{a(a-1)}$,
当a=4时,原式=$\frac{1}{4×(4-1)}=\frac{1}{12}$;
(2)$\frac{1}{a+1}$-$\frac{a+2}{{{a^2}-1}}$÷$\frac{{({a+1})({a+2})}}{{{a^2}-2a+1}}$
=$\frac{1}{a+1}-\frac{a+2}{(a+1)(a-1)}×\frac{(a-1)^{2}}{(a+1)(a+2)}$
=$\frac{1}{a+1}-\frac{a-1}{(a+1)^{2}}$
=$\frac{a+1-a+1}{(a+1)^{2}}$
=$\frac{2}{{a}^{2}+2a+1}$,
∵a2+2a-15=0,
∴a2+2a=15,
∴原式=$\frac{2}{15+1}=\frac{1}{8}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
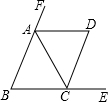 如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
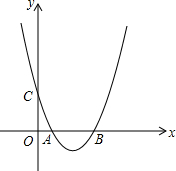 如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 零除以任何数都等于零 | |
| B. | 1除以一个数就等于乘这个数的倒数 | |
| C. | 一个不等于零的有理数除以它的相反数等于-1 | |
| D. | 两数相除,商一定小于被除数 |
查看答案和解析>>
科目:初中数学 来源:2017届内蒙古呼伦贝尔市海拉尔区九年级5月中考模拟考试数学试卷(解析版) 题型:填空题
有这样一组数据 满足以下规律:
满足以下规律:  ,
,  ,
, 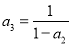 ,…,
,…, 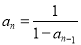 (n≥2且
(n≥2且 为正整数),则a2016的值为___________________.(结果用数字表示)
为正整数),则a2016的值为___________________.(结果用数字表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com