
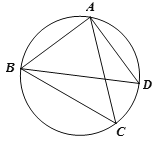
【题目】如图![]() ,点C为△ABD外接圆上的一动点(点C不在
,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
【答案】(1)详见解析;(2)详见解析;(3)DM2=BM2+2MA2,理由详见解析.
【解析】
试题分析:(1)易证△ABD为等腰直角三角形,即可判定BD是该外接圆的直径;(2)如图所示作CA⊥AE,延长CB交AE于点E,再证△ACE为等腰直角三角形,可得AC=AE,再由勾股定理即可得![]() ;利用SAS判定△ABE≌△ADC,可得BE=DC,所以CE=BE+B,所以C=DC+BC=
;利用SAS判定△ABE≌△ADC,可得BE=DC,所以CE=BE+B,所以C=DC+BC=![]() ;(3)延长MB交圆于点E,连结AE、DE,因∠BEA=∠ACB=∠BMA=45°,在△MAE中有MA=AE,∠MAE=90°,由勾股定理可得
;(3)延长MB交圆于点E,连结AE、DE,因∠BEA=∠ACB=∠BMA=45°,在△MAE中有MA=AE,∠MAE=90°,由勾股定理可得![]() ,再证∠BED=90°,在RT△MED中,有
,再证∠BED=90°,在RT△MED中,有![]() ,所以
,所以![]() .
.
试题解析:(1)∵弧AB=弧AB, ∴∠ADB=∠ACB
又∵∠ACB=∠ABD=45° ∴∠ABD=∠ADB=45°
∴∠BAD=90° ∴△ABD为等腰直角三角形
∴BD是该外接圆的直径
(2)如图所示作CA⊥AE,延长CB交AE于点E
∵∠ACB=45°,CA⊥AE
∴△ACE为等腰直角三角形 ∴AC=AE
由勾股定理可知CE2=AC2+AE2=2AC2 ∴![]()
由(1)可知△ABD 为等腰直角三角形
∴AB=AD ∠BAD=90° 又∵∠EAC=90°
∴∠EAB+∠BAC=∠DAC+∠BAC ∴∠EAB=∠DAC
∴在△ABE和△ADC中

∴△ABE≌△ADC(SAS)
∴BE=DC
∴CE=BE+BC=DC+BC=![]()

(3)DM2=BM2+2MA2
延长MB交圆于点E,连结AE、DE
∵∠BEA=∠ACB=∠BMA=45°
∴在△MAE中有MA=AE,∠MAE=90°
∴![]()
又∵AC=MA=AE
∴![]() =
=![]()
又∵![]() =
=![]()
∴![]() -
-![]() +
+![]() =
=![]() -
-![]() +
+![]()
即![]() =
=![]()
∴DE=BC=MB
∵BD为直径
∴∠BED=90°
在RT△MED中,有![]()
∴![]()




 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】先化简再求值
(1)-(9x3-4x2+5)-(-3-8x3+3x2),其中x=-2;
(2)5xy﹣[x2+4xy﹣y2﹣(x2+2xy﹣2y2)]其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,n)在抛物线![]() 上.
上.
(1)若b=1,c=3,①求n的值;
②求出此时二次函数在![]() 上的最小值
上的最小值
(2)若此抛物线经过点B(6,n),且二次函数![]() 的最小值是-4,请画出点P(
的最小值是-4,请画出点P(![]() ,
, ![]() )的纵坐标随横坐标变化的图象,并说明理由.
)的纵坐标随横坐标变化的图象,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b(a<0)的图象与x的交点坐标是(3,0),那么关于x的方程ax+b=0的解是 , 关于x的不等式ax+b>0的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同).
(1)装饰物所占的面积是多少?窗户中能射进阳光的部分的面积是多少(窗框面积忽略不计)?
(2)观察(1)中所得到的结果,它们是单项式还是多项式?次数分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com