
 ��ͼ�����κ���y=-x2+bx+c��ͼ�������ߣ���x�ύ��A��1��0�����ҵ�x=0��x=-2ʱ����Ӧ�ĺ���ֵ��ȣ�
��ͼ�����κ���y=-x2+bx+c��ͼ�������ߣ���x�ύ��A��1��0�����ҵ�x=0��x=-2ʱ����Ӧ�ĺ���ֵ��ȣ����� ��1�������������ߵĶԳ��Եõ������ߵĶԳ���Ϊֱ��x=-1������������x�����һ����������Ϊ��-3��0����Ȼ�����ý���ʽ�������߽���ʽ��
��2������BC��ֱ��x=-1�ڵ�D����DB=DA����������֮���߶���̿��жϴ�ʱDA+DC��С����ADC���ܳ���С���������ô���ϵ�������ֱ��BC�Ľ���ʽ��Ȼ������Ա���Ϊ-1����Ӧ�ĺ���ֵ���ɵõ�D�����ꣻ
��3����MN��y�ύBC��N����ͼ����M��t��-t2-2t+3����-3��x��0������N��t��t+3��������S��BCM=S��MNB+S��NMC�ɵõ���MBC�����=-$\frac{3}{2}$t2-$\frac{9}{2}$t��Ȼ�����ö��κ�����������⣮
��� �⣺��1���ߵ�x=0��x=-2ʱ����Ӧ�ĺ���ֵ��ȣ�
�������ߵĶԳ���Ϊֱ��x=-1��
����������x�����һ����������Ϊ��-3��0����
�������߽���ʽΪy=-��x+3����x-1������y=-x2-2x+3��
��2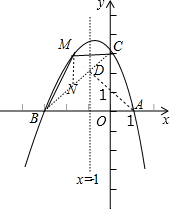 ���ڣ�
���ڣ�
����BC��ֱ��x=-1�ڵ�D����DB=DA��
��DC+DA=DC+DB=BC��
���ʱDA+DC��С����ADC���ܳ���С��
��x=0ʱ��y=-x2-2x+3=3����C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+m��
��B��-3��0����C��0��3�������$\left\{\begin{array}{l}{-3k+m=0}\\{m=3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=1}\\{m=3}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=x+3��
��x=-1ʱ��y=x+3=2��
��D��������-1��2����
��3����MN��y�ύBC��N����ͼ��
��M��t��-t2-2t+3����-3��t��0������N��t��t+3����
S��BCM=S��MNB+S��NMC
=$\frac{1}{2}$•3•MN
=$\frac{3}{2}$��-t2-2t+3-t-3��
=-$\frac{3}{2}$t2-$\frac{9}{2}$t
=-$\frac{3}{2}$��t+$\frac{3}{2}$��2+$\frac{27}{8}$��
�൱t=-$\frac{3}{2}$ʱ����MBC����������ֵΪ$\frac{27}{8}$��
��ʱM������Ϊ��-$\frac{3}{2}$��$\frac{15}{4}$����
���� ���⿼������������x��Ľ��㣺������κ���y=ax2+bx+c��a��b��c�dz�����a��0����x��Ľ�����������ת��Ϊ�����x��һԪ���η��̣�Ҳ�����˶��κ��������ʺ����·�����⣮


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��OA��x���ϣ�OB��y���ϣ�OA=4��OB=3����C�ڱ�OA�ϣ�AC=1����P��Բ��P���߶�BC�ϣ��ҡ�P���AB��AO�����У�������������y=$\frac{k}{x}$��k��0����ͼ��Բ��P����k��ֵ�ǣ�������
��ͼ��OA��x���ϣ�OB��y���ϣ�OA=4��OB=3����C�ڱ�OA�ϣ�AC=1����P��Բ��P���߶�BC�ϣ��ҡ�P���AB��AO�����У�������������y=$\frac{k}{x}$��k��0����ͼ��Բ��P����k��ֵ�ǣ�������| A�� | $-\frac{5}{4}$ | B�� | $-\frac{5}{3}$ | C�� | $-\frac{5}{2}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
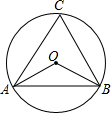 ��ͼ����ABC�ڽ��ڡ�O������AOB=110�㣬���ACB�Ķ����ǣ�������
��ͼ����ABC�ڽ��ڡ�O������AOB=110�㣬���ACB�Ķ����ǣ�������| A�� | 70�� | B�� | 60�� | C�� | 55�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 264��103 | B�� | 2.64��104 | C�� | 2.64��105 | D�� | 0.264��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=x+b��˫����y=$\frac{k}{x}$�ཻ��A��B���㣬��֪A��2��5����
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=x+b��˫����y=$\frac{k}{x}$�ཻ��A��B���㣬��֪A��2��5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com