
当a>0且x>0时,因为 ≥0,所以
≥0,所以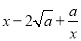 ≥0,从而
≥0,从而 (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为 .
.
(1)已知函数y1=x(x>0)与函数 ,则当x= 1 时,y1+y2取得最小值为 2 .
,则当x= 1 时,y1+y2取得最小值为 2 .
(2)已知函数y1=x+1(x>﹣1)与函数 ,求
,求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
(1)1;2.(2)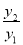 的最小值为4,相应的x的值为1.
的最小值为4,相应的x的值为1.
【解析】
试题分析:(1)可以直接套用题意所给的结论,即可得出结果.
(2)先得出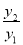 的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.
的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.
试题解析:(1)∵函数 ),由上述结论可知:当
),由上述结论可知:当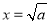 时,该函数有最小值为
时,该函数有最小值为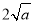 .
.
∴函数y1=x(x>0)与函数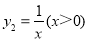 ,则当x=
,则当x=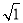 =1,即x=1时,y1+y2取得最小值为2.
=1,即x=1时,y1+y2取得最小值为2.
(2)∵已知函数y1=x+1(x>﹣1)与函数y2=(x+1)2+4(x>﹣1),
∴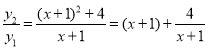 (x>﹣1),
(x>﹣1),
∴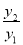 有最小值为
有最小值为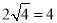 .
.
当 ,即x=1时取得该最小值.
,即x=1时取得该最小值.
检验:x=1时,x+1=2≠0,
故x=1是原方程的解.
所以,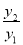 的最小值为4,相应的x的值为1.
的最小值为4,相应的x的值为1.
考点:二次函数综合题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
(本题满分6分)设 、
、 是方程
是方程 的两个实数根,不解方程,求下列代数式的值.
的两个实数根,不解方程,求下列代数式的值.
(1) ; (2)
; (2)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月检测数学试卷(解析版) 题型:填空题
(本题满分12分)问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点 、
、 、
、 确定的圆为⊙
确定的圆为⊙ .
.
(1)当 、
、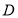 在线段
在线段 的同侧时,
的同侧时,

如图①,若点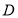 在⊙
在⊙ 上,此时有
上,此时有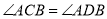 ,理由是 ;
,理由是 ;
如图②,若点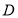 在⊙
在⊙ 内,此时有
内,此时有
 ;
;
如图③,若点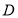 在⊙
在⊙ 外,此时有
外,此时有
 .(填“
.(填“ ”、“
”、“ ”或“
”或“ ”);
”);
由上面的探究,请直接写出 、
、 、
、 、
、 四点在同一个圆上的条件: .
四点在同一个圆上的条件: .
类比学习:(2)仿照上面的探究思路,请探究:当 、
、 在线段
在线段 的异侧时的情形.
的异侧时的情形.

如图④,此时有 ,如图⑤,此时有 ,
如图⑥,此时有 .
由上面的探究,请用文字语言直接写出 、
、 、
、 、
、 四点在同一个圆上的条件:
四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知: 如图,
如图, 是⊙
是⊙ 的直径,点
的直径,点 在⊙
在⊙ 上,求作:
上,求作: .
.
作法:①连接 ,
, ;
;
②在  上任取异于
上任取异于 、
、 的一点
的一点 ,连接
,连接 ,
, ;
;
③ 与
与 相交于
相交于 点,延长
点,延长 、
、 ,交于
,交于 点;
点;
④连接 、
、 并延长,交直径
并延长,交直径 于
于 ;
;
⑤连接 、
、 并延长,交⊙
并延长,交⊙ 于N.连接
于N.连接 . 则
. 则 .
.
请按上述作法在图④中作图,并说明 的理由.(提示:可以利用(2)中的结论)
的理由.(提示:可以利用(2)中的结论)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月检测数学试卷(解析版) 题型:填空题
 年南京青奥会某项目
年南京青奥会某项目 名礼仪小姐的身高如下(单位:
名礼仪小姐的身高如下(单位: ):
): ,
, ,
,
 ,
, ,
, ,
, ,则她们身高的极差是
,则她们身高的极差是  .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月检测数学试卷(解析版) 题型:选择题
把抛物线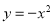 向左平移
向左平移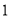 个单位,然后向上平移
个单位,然后向上平移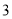 个单位,则平移后抛物线的解析式为( ).
个单位,则平移后抛物线的解析式为( ).
A.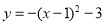 B.
B.
C.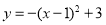 D.
D.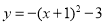
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:解答题
△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:

①b2﹣4ac>0;
②2a+b<0;
③4a﹣2b+c=0;
④a:b:c=﹣1:2:3.
其中正确的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末考试数学试卷(解析版) 题型:填空题
一个容量为n的样本分成若干组,已知某组的频数和频率分别是30和0.25,则n =________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省容城镇三闾学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
将一元二次方程5x2-1=4x化成一般形式后,一次项系数和二次项系数分别为( )
A.5,-1 B.5,4 C.-4,5 D.5x2,-4x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com