
如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点(点A在点B的左侧)。
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。
解:(1)∵将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2,
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,-4)。
∴抛物线C2的顶点坐标为(1,-4)。
∴抛物线C2的解析式为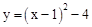 ,即
,即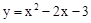 。
。
(2)证明:由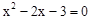 解得
解得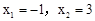 ,
,
∵点A在点B的左侧,∴A(-1,0),B(3,0),AB=4。
∵抛物线C2的对称轴为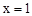 ,顶点坐标D为(1,-4),∴CD=4。AC=CB=2。
,顶点坐标D为(1,-4),∴CD=4。AC=CB=2。
将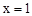 代入y=x2+3得y=4,∴E(1, 4),CE=DE。
代入y=x2+3得y=4,∴E(1, 4),CE=DE。
∴四边形ADBE是平行四边形。
∵ED⊥AB,∴四边形ADBE是菱形。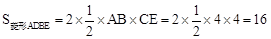 。
。
(3)存在。分AB为平行四边形的边和对角线两种情况:
①当AB为平行四边形的一边时,如图,
设F(1,y),
∵OB=3,∴G1(-2,y)或G2(4,y)。
∵点G在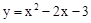 上,
上,
∴将x=-2代入,得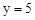 ;将x=4代入,得
;将x=4代入,得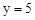 。
。
∴G1(-2,5),G2(4,5)。
②当AB为平行四边形的一对角线时,如图,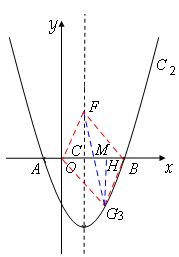
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM=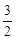 ,CM=
,CM= 。
。
∵△CFM≌△HGM(AAS),∴HM=CM= 。∴OH=2。
。∴OH=2。
∴G3(2,-y)。
∵点G在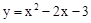 上,
上,
∴将(2,-y)代入,得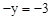 ,即
,即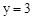 。
。
∴G3(2,-3)。
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(-2,5),G2(4,5),G3(2,-3)。
解析试题分析:(1)根据平移的性质,写出平移后的顶点坐标即可得出抛物线C2的解析式。
(2)求出点A、B、D、E的坐标,即可根据对角线互相垂直平分的四边形是菱形的判定得到证明;从而根据菱形的性质求出面积。
(3)分AB为平行四边形的边和对角线两种情况讨论即可。


科目:初中数学 来源: 题型:解答题
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川眉山11分)如图,在平面直角坐标系中,点A、B在x轴上,点C、D在y轴上,且OB=OC=3,OA=OD=1,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,直线AD与抛物线交于另一点M.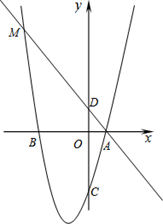
(1)求这条抛物线的解析式;
(2)P为抛物线上一动点,E为直线AD上一动点,是否存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
(3)请直接写出将该抛物线沿射线AD方向平移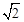 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年广东梅州10分)如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.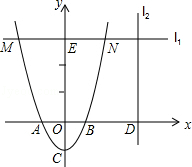
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线的顶点为(0,4)且与x轴交于(﹣2,0),(2,0).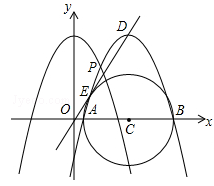
(1)直接写出抛物线解析式;
(2)如图,将抛物线向右平移k个单位,设平移后抛物线的顶点为D,与x轴的交点为A、B,与原抛物线的交点为P.
①当直线OD与以AB为直径的圆相切于E时,求此时k的值;
②是否存在这样的k值,使得点O、P、D三点恰好在同一条直线上?若存在,求出k值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)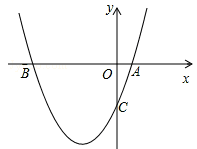
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=﹣x2+bx+c.点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.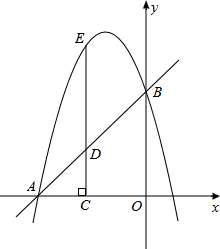
(1)求抛物线的解析式.
(2)当DE=4时,求四边形CAEB的面积.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求此点D坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系: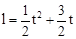 (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y= (x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )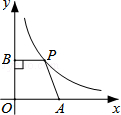
| A.逐渐增大 | B.不变 | C.逐渐减小 | D.先增大后减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com