
分析 (1)根据零指数幂、负整数指数幂、绝对值可以解答本题;
(2)根据分式的除法和减法可以解答本题.
解答 解:(1)$\sqrt{64}-(\sqrt{5}-1)^{0}+12×{3}^{-1}-|-5|$
=8-1+4-5
=6;
(2)1-$\frac{x-1}{x}$÷$\frac{{x}^{2}-1}{{x}^{2}+2x}$
=$1-\frac{x-1}{x}÷\frac{{({x+1})({x-1})}}{{x({x+2})}}$
=1-$\frac{x-1}{x}•\frac{x(x+2)}{(x+1)(x-1)}$
=$1-\frac{x+2}{x+1}$
=$-\frac{1}{x+1}$.
点评 本题考查分式的混合运算、实数的运算、零指数幂、负整数指数幂、绝对值,解答本题的关键是明确它们各自的计算方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
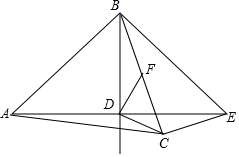 如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com