
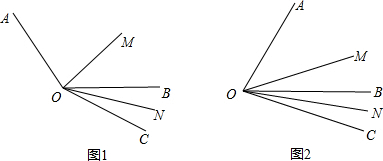
分析 (1)根据∠AOB=120°,∠BOC=30°,可得∠AOC=∠AOB+∠BOC=120°+30°=150°,再利用OM是∠AOC的平分线,ON是∠BOC的平分线,即可求得答案;
(2)根据∠MON=∠MOC-∠NOC,又利用∠AOB=120°,∠BOC=β°,由(1)可得出答案;
(3)利用(1)(2)的计算方法得出规律即可.
解答 解:(1)∵∠AOB=120°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=120°+30°=150°,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,
∴∠MON=∠MOC-∠NOC=75°-15°=60°,
(2)当∠AOB=120°,∠BOC=β°时,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(120+β)°-$\frac{1}{2}$β°=60°;
(3)由(1)(2)可知:
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(α+β)°-$\frac{1}{2}$β°=$\frac{1}{2}$α°.
∠MON的度数始终等于∠AOB角度的一半.
点评 本题主要考查角的计算和角平分线的定义等知识点的理解和掌握,难度不大,属于基础题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:解答题
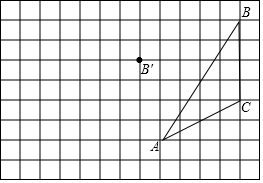 画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
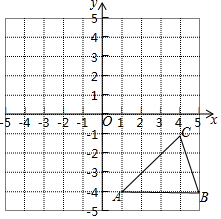 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
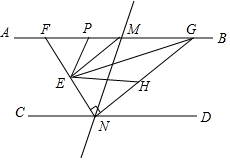 如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com