
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
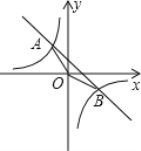
【答案】(1)一次函数的解析式为y=﹣x+2;(2)S△AOB=6;(3)由图象可知:一次函数的函数值大于反比例函数的函数值时x的取值范围是x<﹣2或0<x<4.
【解析】试题分析:(1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;
(2)设直线AB与y轴交于C,找出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论;
(3)观察函数图象,根据图象的上下关系即可找出不等式的解集.
试题解析:(1)令反比例函数y=-![]() 中x=-2,则y=4,
中x=-2,则y=4,
∴点A的坐标为(-2,4);
反比例函数y=-![]() 中y=-2,则-2=-
中y=-2,则-2=-![]() ,解得:x=4,
,解得:x=4,
∴点B的坐标为(4,-2).
∵一次函数过A、B两点,
∴![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=-x+2.
(2)设直线AB与y轴交于C,
令为y=-x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB=![]() OC(xB-xA)=
OC(xB-xA)=![]() ×2×[4-(-2)]=6.
×2×[4-(-2)]=6.
(3)观察函数图象发现:
当x<-2或0<x<4时,一次函数图象在反比例函数图象上方,
∴一次函数的函数值大于反比例函数的函数值时x的取值范围为x<-2或0<x<4.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
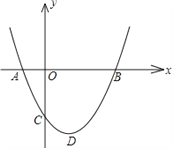
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:①2a+b=0;②a+b+c>0;③4a+b+c>0;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有三个.那么,其中正确的结论是_____.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有三个.那么,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强市民的节水意识,某市对居民用水实行“阶梯收费”:规定每户每月不超过月用水标准部分的水价为1.5元/吨,超过月用水标准量部分的水价为2.5元/吨.该市小明家5月份用水12吨,交水费20元.请问:该市规定的每户月用水标准量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在等腰三角形中,对于顶角的每一个确定的值,其底边与腰的比值都是唯一确定的,这个比值是顶角的正对函数.例如:图①,在△ABC中,AB=AC,顶角A的正对函数记作sadA,sadA=![]() 或sadA=
或sadA=![]() .
.
(1)在图①中,若∠B=60°,则sadA= .
(2)如图②,在△ABC中,AB=AC,若∠BAC=120°,求sad∠BAC.
(3)在Rt△ABC中,∠C=90°,sinA=![]() ,直接写出三个内角的正对函数值.
,直接写出三个内角的正对函数值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com