
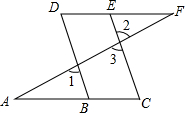
 完成下列推理过程
完成下列推理过程 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:选择题
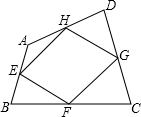 如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )
如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )| A. | 一定不是平行四边形 | B. | 一定不是中心对称图形 | ||
| C. | 可能是轴对称图形 | D. | 当AC=BD时它是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
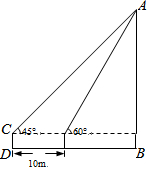 如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB.
如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
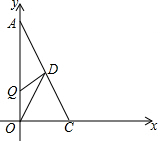 如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.
如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
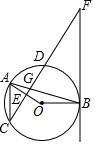 如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
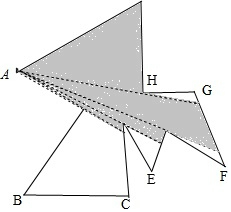 如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )
如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )| A. | E处 | B. | F处 | C. | G处 | D. | H处 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com