
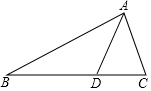
 如图,在△ABC中,AC=4,D为BC边上的一点,CD=2,且△ADC与△ABD的面积比为1:3.
如图,在△ABC中,AC=4,D为BC边上的一点,CD=2,且△ADC与△ABD的面积比为1:3.分析 (1)由三角形的面积关系求出BD=3DC=6,得出BC=BD+CD=8,在△ADC与△ABD中,$\frac{BC}{AC}=\frac{AC}{BD}=2$,∠BCA=∠ACD,即可得出结论;
(2)由相似三角形的性质得出$\frac{AD}{DC}$=$\frac{AB}{AC}$,即可求出AD的长.
解答 (1)证明:∵CD=2,且△ADC与△ABD的面积比为1:3.
∴BD=3DC=6,
∴BC=BD+CD=8,
∴在△ADC与△ABD中,$\frac{BC}{AC}=\frac{AC}{BD}=2$,∠BCA=∠ACD.
∴△ADC∽△BAC.
(2)解:∵△ADC∽△BAC,
∴$\frac{AD}{DC}$=$\frac{AB}{AC}$,
又∵AB=8,AC=4,CD=2.
∴AD=$\frac{2×8}{4}$=4.
点评 本题考查了相似三角形的判定与性质、三角形的面积;证明三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
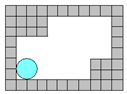 将半径为2cm的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的内侧滚动一周,回到开始位置后,圆心经过的路线的长度为 ( )(精确到0.01cm)
将半径为2cm的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的内侧滚动一周,回到开始位置后,圆心经过的路线的长度为 ( )(精确到0.01cm)| A. | 36cm | B. | 42.28cm | C. | 40.28cm | D. | 40cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
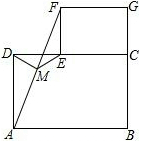 猜想与证明:
猜想与证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
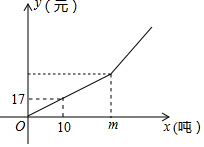 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:| 月份 | 用水量x(吨) | 水费y(元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com