
 如图,?ABCD中,AB=3,BC=5,∠ABC的平分线与AD相交于点E,求DE的长.
如图,?ABCD中,AB=3,BC=5,∠ABC的平分线与AD相交于点E,求DE的长. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
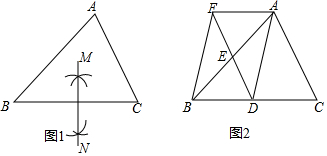
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
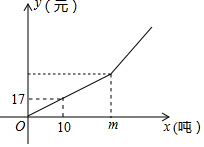 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:| 月份 | 用水量x(吨) | 水费y(元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
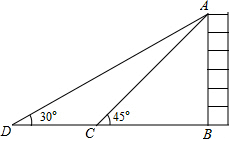 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.
如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com