圆锥底面圆的周长为6π,高为4,则其全面积为( )
A.24π
B.9π
C.15π
D.15π+9
【答案】
分析:由圆锥底面圆的周长为6π,得到半径OB=3,然后利用勾股定理得到母线长为5,圆锥的侧面展开图为扇形,母线为扇形的半径,底面圆的周长为扇形的弧长,最后利用扇形的面积公式和圆的面积公式进行计算即可得到圆锥的全面积.
解答: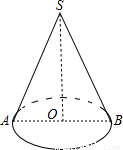
解:如图,SO=4,
∵圆锥底面圆的周长为6π,
∴2•π•OB=6π,
∴OB=3,
∴SB=
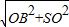
=
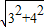
=5,
∴圆锥的侧面积=

•6π•5=15π,
圆锥的底面圆的面积=3
2•π=9π,
∴圆锥的全面积=15π+9π=24π.
故选A.
点评:本题考查了圆锥的有关计算:圆锥的侧面展开图为扇形,母线为扇形的半径,底面圆的周长为扇形的弧长.也考查了扇形的面积公式以及勾股定理.

 解:如图,SO=4,
解:如图,SO=4,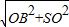 =
=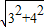 =5,
=5, •6π•5=15π,
•6π•5=15π,

 53随堂测系列答案
53随堂测系列答案