【题目】已知关于x的一元二次方程x2+2x﹣（m﹣2）＝0有实数根．
（1）求m的取值范围；
（2）若方程有一个根为x＝1，求m的值及另一个根．
【答案】（1）
；（2）
的值为
，方程的另一个根为
．
【解析】
（1）由方程有实数根结合根的判别式即可得出关于m的一元一次不等式，解之即可得出m的取值范围；
（2）将x＝1代入原方程求出m值，再将m的值代入原方程利用十字相乘法解一元二次方程即可得出方程的另一个根．
（1）∵关于x的一元二次方程x2+2x﹣（m﹣2）＝0有实数根，∴△＝b2﹣4ac＝22﹣4×1×[﹣（m﹣2）]＝4m﹣4≥0，解得：m≥1．
（2）将x＝1代入原方程，1+2﹣（m﹣2）＝0，解得：m＝5，∴原方程为x2+2x﹣3＝（x﹣1）（x+3）＝0，解得：x1＝1，x2＝﹣3，∴m的值为5，方程的另一个根为x＝﹣3．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】经市场调研发现：某品牌童装平均每天可售出 20 件，每件盈利 40元．在每件降价幅度不超过 18 元的情况下，若每件童装降价 1 元，则每天可多售出 2 件，设降价 x 元．
（1）降价 x 元后，每件童装盈利是多少元，每天销售量是多少件；
（2）要想每天销售这种童装盈利 1200 元，那么每件童装应降价多少元？
（3）每天能盈利 1800 元吗？如果能，每件童装应降价多少元？如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝－x2＋bx＋c经过点B(－1，0)和点C(2，3)．
(1)求此抛物线的函数表达式；
(2)如果此抛物线上下平移后过点(－2，－1)，请直接写出平移的方向和平移的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
的图象过A（2，0），B（0，-1）和C（4，5）三点。
（1）求二次函数的解析式；
（2）设二次函数的图象与
轴的另一个交点为D，求点D的坐标；
（3）在同一坐标系中画出直线
，并写出当在什么范围内时，一次函数的值大于二次函数的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程．原计划每天拆迁
，因为准备工作不足，第一天少拆迁了
．从第二天开始，该工程队加快了拆迁速度，第三天拆迁了
．求：
该工程队第一天拆迁的面积；
若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同，求这个百分数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某青年旅社有60间客房供游客居住，在旅游旺季，当客房的定价为每天200元时，所有客房都可以住满．客房定价每提高10元，就会有1个客房空闲，对有游客入住的客房，旅社还需要对每个房间支出20元/每天的维护费用，设每间客房的定价提高了x元．
（1）填表（不需化简）
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
（2）若该青年旅社希望每天纯收入为14000元且能吸引更多的游客，则每间客房的定价应为多少元？（纯收入=总收入﹣维护费用）
查看答案和解析>>
科目：初中数学 来源： 题型：
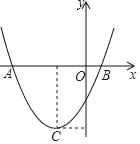
【题目】如图，二次函数y＝ax2+bx+c（a≠0）的图象的顶点C的坐标为（﹣1，﹣3），与x轴交于A（﹣3，0）、B（1，0），根据图象回答下列问题：
（1）写出方程ax2+bx+c＝0的根；
（2）写出不等式ax2+bx+c＞0的解集；
（3）写出y随x的增大而减少时自变量x的取值范围；
（4）若方程ax2+bx+c＝k有实数根，写出实数k的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知A（﹣4，2），B（2，﹣4）是一次函数y=kx+b的图象和反比例函数y=
图象的两个交点．
（1）求反比例函数和一次函数的表达式；
（2）将一次函数y=kx+b的图象沿y轴向上平移n个单位长度，交y轴于点C，若S△ABC=12，求n的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
